Добрый день! Давайте разберем каждый из заданий по порядку.
1. Найдите значение выражения 3,5 • 23 – 34.
Для начала нужно выполнить умножение: 3,5 • 23 = 80,5.
После этого вычитаем 34: 80,5 - 34 = 46,5.
Ответ: 46,5.
5. Вычислите:
Нет выражения, которое нужно вычислить. Пожалуйста, уточните номер задания.
6. Упростите выражение 128х2у3 • (–1/4 • xy5)3.
Сначала упростим два умножения: 128х2у3 • (–1/4 • xy5) = -32х2у3 • xy5.
Затем перемножаем: -32х2у3 • xy5 = -32x(2+1) • y(3+5) = -32х3у8.
Ответ: -32х3у8.
7. Вместо звёздочки запишите такой многочлен, чтобы образовалось тождество: (4x2 – 2xy + y2) – (*) = 3x2 + 2xy.
В данном случае необходимо найти такой многочлен, который при вычитании из (4x2 – 2xy + y2) даст (3x2 + 2xy).
Получается, что (*), то есть искомый многочлен равен y2 - 3x2.
Ответ: y2 - 3x2.
8. Докажите, что значение выражения (11n + 39) – (4n + 11) кратно 7 при любом натуральном значении n.
Для доказательства нужно вычислить значение данного выражения и проверить, делится ли оно на 7 при любом натуральном значении n.
Вычисляем выражение: (11n + 39) – (4n + 11) = 11n + 39 - 4n - 11 = (11n - 4n) + (39 - 11) = 7n + 28.
У нас получается выражение 7n + 28, которое делится на 7 без остатка при любом натуральном значении n.
Таким образом, значение выражения (11n + 39) – (4n + 11) кратно 7 при любом натуральном значении n.
9. Известно, что 6ab5 = –7. Найдите значение выражения: 1) 18ab5; 2) 6a2b10.
Исходное уравнение 6ab5 = –7 можно переписать в виде: ab5 = –7/6.
1) Значение выражения 18ab5: 18ab5 = 18 • (–7/6) = –21.
2) Значение выражения 6a2b10: 6a2b10 = 6 • a2 • b10 = 6 • (–7/6)2 • (–7/6)10 = 6 • (49/36) • (1/46656) = 1/216.
Ответы: 1) –21; 2) 1/216.
Это были ответы на вопросы из Варианта 1. Если у вас есть вопросы по конкретным заданиям, пожалуйста, задавайте их.
Для того, чтобы система уравнений имела единственное решение, должно быть выполнено следующее условие: определитель матрицы коэффициентов системы должен быть отличен от нуля.
Итак, у нас дано уравнение 4x + 8y = 20. Задача заключается в выборе второго уравнения из списка, чтобы система имела единственное решение (11; -3).
Проверим каждое из предложенных уравнений.
1. 7x + 8y = 4:
Коэффициент при x в данном уравнении равен 7 и не совпадает с коэффициентом при x в исходном уравнении, который равен 4. Поэтому данное уравнение не подходит.
2. 6x + 11y = 8:
Коэффициент при x в данном уравнении равен 6 и не совпадает с коэффициентом при x в исходном уравнении, который равен 4. Поэтому данное уравнение не подходит.
3. 3x + 7y = 12:
Коэффициент при x в данном уравнении равен 3 и не совпадает с коэффициентом при x в исходном уравнении, который равен 4. Поэтому данное уравнение не подходит.
4. 7x - 5y = 3:
Коэффициент при x в данном уравнении равен 7 и не совпадает с коэффициентом при x в исходном уравнении, который равен 4. Поэтому данное уравнение не подходит.
5. 45x - 31y = 13:
Коэффициент при x в данном уравнении равен 45 и не совпадает с коэффициентом при x в исходном уравнении, который равен 4. Поэтому данное уравнение не подходит.
Осталось последнее уравнение:
6. x - y = 3:
Коэффициент при x в данном уравнении равен 1 и совпадает с коэффициентом при x в исходном уравнении, который равен 4.
Коэффициент при y в данном уравнении равен -1 и совпадает с коэффициентом при y в исходном уравнении, который равен 8.
Проверим теперь, подходит ли найденное уравнение для задачи, подставив в него координаты решения (11; -3):
11 - (-3) = 3
14 = 3
Увы, получаем неравенство, что означает, что уравнение x - y = 3 не подходит для данной задачи.
Итак, из всех предложенных уравнений, единственное уравнение, которое подходит для системы с решением (11; -3), - это 7x + 8y = 4.
Два варианта первой тройки членов ар. прогрессии.
Объяснение:
Для арифметической прогрессии справедливо
Нам известно:
Выразим а2, а4, а5 через а1 и b:
То есть для первого равенства:
Для второго:
Запишем это в системе:
Решим 1 уравнение системы
Отсюда:
То есть имеем 2 варианта решения:
1)и такие первые три члена арифм.прогрессии:
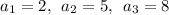
2)и такие первые три члена арифм.прогрессии
ПРОВЕРКА:
1) Если а1 = 2, b = 3:
2) Если а1 = 14, b = -3: