
а - длина прямоугольника
b - ширина прямоугольника
а - ? см, на 4 см >, чем b
b - ? см
S=60 см²
Р - ? см
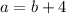
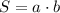

подставим известные величины
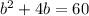
перенесём всё в левую часть и приравняем уравнение к нулю, при этом не забываем сменить знак на противоположный
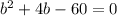
Квадратное уравнение имеет вид: 
Cчитаем дискриминант:
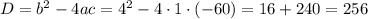
Дискриминант положительный
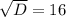
Уравнение имеет два различных корня:
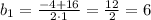
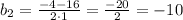
не удовлетворяет условию задачи, так как сторона прямоугольника не может быть отрицательной
следовательно  (см) - ширина прямоугольника.
(см) - ширина прямоугольника.
 (см) - длина прямоугольника.
(см) - длина прямоугольника.
 (см)
(см)
ответ: 32 см периметр прямоугольника.
а - длина прямоугольника
b - ширина прямоугольника
а - ? см, на 4 см >, чем b
b - ? см
S=60 см²
Р - ? см
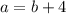
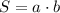
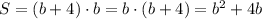
подставим известные величины
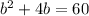
перенесём всё в левую часть и приравняем уравнение к нулю, при этом не забываем сменить знак на противоположный
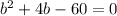
Квадратное уравнение имеет вид: 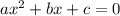
Cчитаем дискриминант:
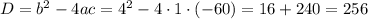
Дискриминант положительный
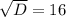
Уравнение имеет два различных корня:
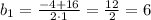
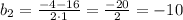
не удовлетворяет условию задачи, так как сторона прямоугольника не может быть отрицательной
следовательно 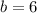 (см) - ширина прямоугольника.
(см) - ширина прямоугольника.
 (см) - длина прямоугольника.
(см) - длина прямоугольника.
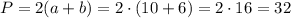 (см)
(см)
ответ: 32 см периметр прямоугольника.
Объяснение:
Это приведённое квадратное уравнение. Применяя теорему Виета, получаем:
Решаем уравнение по теореме Виета:
Вернёмся к замене: