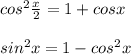
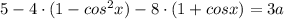
Получаем квадратное уравнение относительно
cosx=t
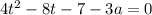
Это уравнение имеет хотя бы один корень, если D ≥0
D=64+16(7+3a)=16(11+3a)
D≥0⇒ 11+3a≥0⇒ a≥ -11/3
t₁=1- (√(11+3а))/2 или t₂=1+ (√(11+3а))/2
Обратная замена приводит к уравнениям вида cos=t₁ или cosx=t₂
Чтобы эти уравнения имели хотя бы один корень, необходимо, что бы
-1 ≤ t₁ ≤1 или -1 ≤ t₂ ≤1
Решаем неравенства:
-1 ≤1+ (√(11+3а))/2 ≤1
-2≤√(11+3а))/2≤0
-4≤√(11+3а)≤0
Решением неравенства является
11+3a=0
a=-11/3
t₁=t₂=1/2
cosx=1/2
x=±(π/3)+2πn, n∈Z
Неравенство
-1 ≤1- (√(11+3а))/2 ≤1
также приводит к ответу a=-11/3
О т в е т. При а=-11/3
x=±(π/3)+2πn, n∈Z
Как добавить хороший ответ
ДОБАВИТЬ СВОЙ ОТВЕТ
Задание
Графіком функції f називають *
геометричну фігуру, яка складається з усіх точок коорди-натної площини, абсциси яких дорівнюють усім значенням аргу-менту, а ординати – відповідним зна-ченням функції f
геометричну фігуру, яка складається з усіх точок координатної площини, абсциси яких дорівнюють усім значенням функції f, а ординати – відпо-відним значенням аргументу
геометричну фігуру, яка складається з усіх точок координатної прямої, абсциси яких дорівнюють усім значенням аргументу, а ординати – вдвічі більші
геометричну фігуру, яка складається з усіх точок координатної площини, абсциси яких дорівнюють значенням функції f
-1<=cos x<=1
-4<=4cos x<=4
-4<=-4cos x<=4
-1<=-4cos x+3<=7
ответ: От -1 до 7, включая концы