Объяснение:
5x^2-6x+8=0
D=36-4×5×8=36-160=-124
D{0
Окружность с центром в т. O и D = 68. Хорда AB.
Расстояние OM = 30 от т. O до прямой AB.
Найти:AB - ?
Решение:Заметим, что OM ⊥ AB (так как OM - это расстояние от т. О до прямой AB - длина перпендикуляра из точки О к прямой AB).
Пусть отрезок OM лежит на радиусе OC рассматриваемой окружности. Тогда OC, как радиус, перпендикулярный хорде, пересекает эту хорду ровно в ее середине: AM = BM.
Рассмотрим прямоугольные треугольники, равные по первому признаку (или же по двум катетам OM = OM и AM = BM): ΔAOM = ΔBOM.
OA = OB = D / 2 = 68 / 2 = 34, как радиусы.
OM = 30, по условию.
Применим теорему Пифагора, например, к ΔAOM:
AM² + OM² = AO²
AM² = AO² - OM²
AM² = 34² - 30²
AM² = 256
AM = 16
Значит:
AB = AM + BM = AM + AM = 16 + 16 = 32.
Задача решена!
ответ: 32.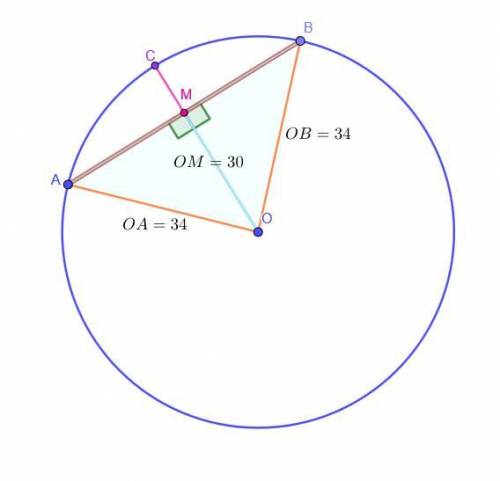
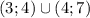
Объяснение:
Решим первое неравенство. ОДЗ:
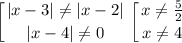
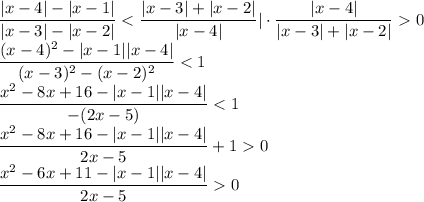
Если x < 1 или x ≥ 4, то модули раскрываются с одним знаком, произведение подмодульных выражений положительно:
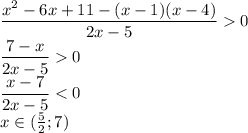
Учитывая, что x < 1 или x ≥ 4, а также учитывая ОДЗ,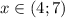 
Если 1 ≤ x < 4, то модули раскрываются с разным знаком, произведение подмодульных выражений отрицательно:
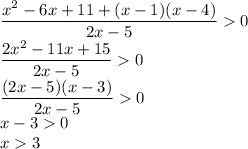
Учитывая, что 1 ≤ x < 4 и ОДЗ,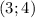 
.
Объединяя полученные промежутки, получаем, что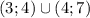
Решим второе неравенство. Пусть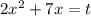 
. Тогда
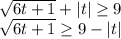
Если правая часть отрицательна, то неравенство выполняется на ОДЗ, так как квадратный корень всегда неотрицателен:
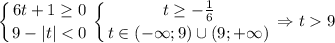
Если правая часть неотрицательна, то обе части можно возвести в квадрат:
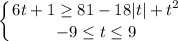
Если t ≥ 0, то модуль раскрывается с плюсом, первое неравенство имеет вид:
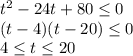
Если t < 0, то модуль раскрывается с минусом, неравенство имеет вид:
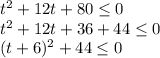
Сумма неотрицательного и положительного чисел не может быть неположительной. В данном случае решений нет.
Учитывая -9 ≤ t ≤ 9, решением данного случая является ![t\in[4;9]](/tpl/images/1358/7181/70120.png)
Объединив оба случая, получаем t ≥ 4,
![2x^2+7x-4\geq 0\\(x+4)(2x-1)\geq 0\\x\in(-\infty;-4]\cup[\frac{1}{2};+\infty)](/tpl/images/1358/7181/42d33.png)
Пересечём полученные решения: ответом будет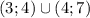
ответ: нет корней
Объяснение:
5х²-6х+8=0
х₁,₂=(3±√(9-40))/5
D<0