Все решение в фото
Объяснение:
Как-то так
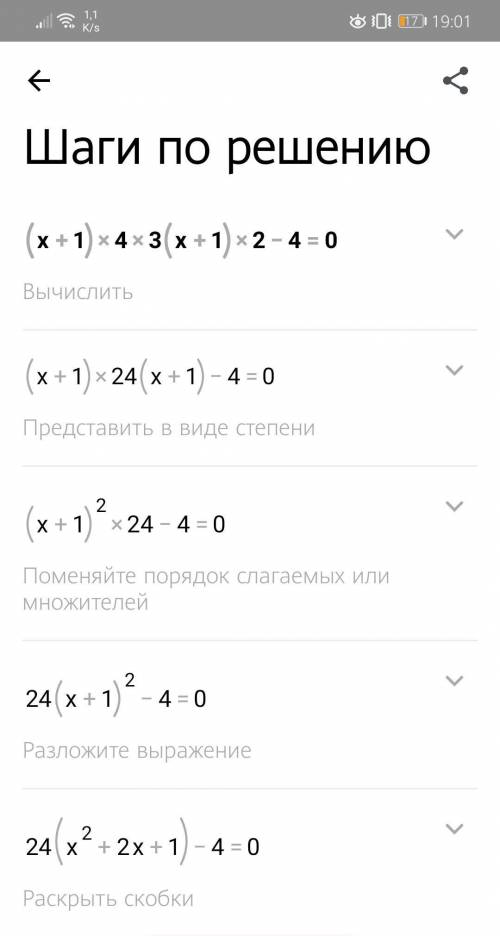
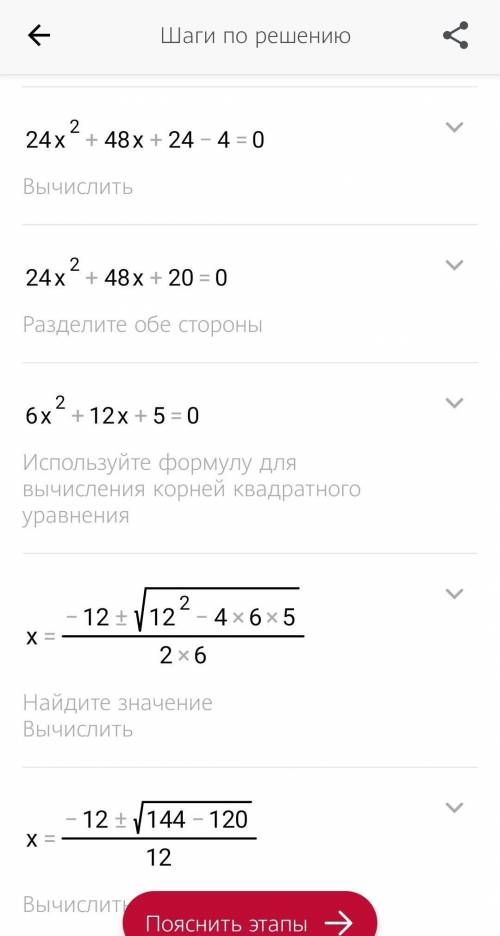
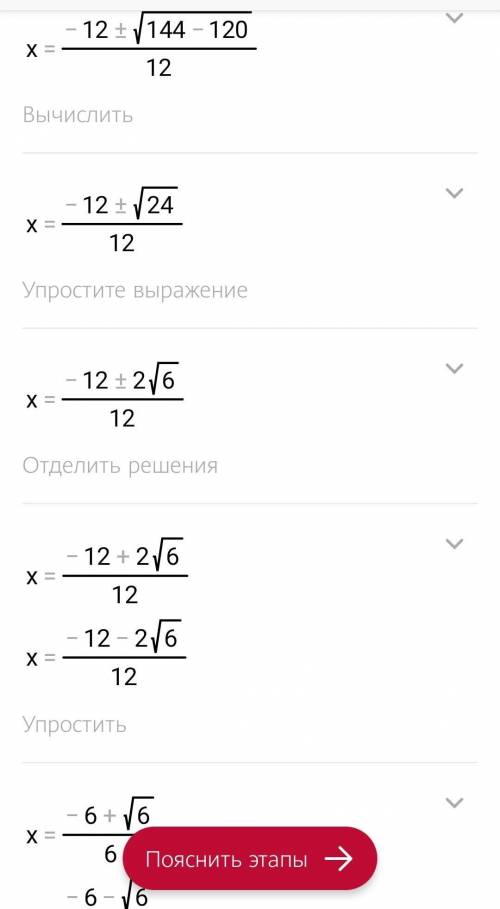
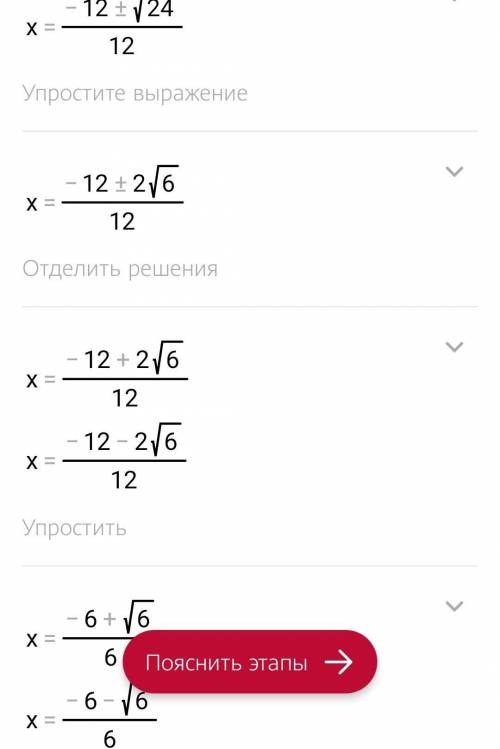
найдем производную f´(x)=( x^4-2x^2-3)´=( x^4)´-2(x^2)´-(3)´=4х³-4х-0=4х³-4х=4х(х²-1)=4х(х-1)(х+1) найдем критические точки, т.е f´(x)=0 4х(х-1)(х+1)=0 х=0 или х=1 или х=-1 ++→х f´(-2)= 4*(--+1)= 4*(-)< 0 ( нас интересует знак, а не число) f´(-0,5)= 4*(-0,,5-,5+1)= 4*(-0,,5)*0,5> 0 f´(0,5)= 4*0,5*(0,5-1)(0,5+1)=4*0,5*(-0,5)*1,5< 0 f´(2)= 4*2*(2-1)(2+1)=4*2*1*3> 0 в точке х=-1 производная меняет знак с – на +, значит это точка минимума; в точке х=0 производная меняет знак с +на -, значит это точка максимума; в точке х=1 производная меняет знак с – на +, значит это точка минимума; 2) f(x)= x^2+3x /x+4 найдем производную f´(x)=( x^2+3x /x+4)´=( x^2+3x)´(х+4)- (x^2+3x)( x+4)´/ (x+4)² =(2х+3)(х+²+3х)*1/(х+4)²=(2х²+8х+3х+12-х²-3х)/(х+4)²=(х²+8х+12)/(х+4)²=(х+2)(х+6)/(х+4)² найдем критические точки, т.е f´(x)=0 (х²+8х+12)/(х+4)²=0 х²+8х+12=0 и х+4≠0; х≠-4 д=8²-4*1*12=64-48=16; х₁=-8+√16/2=-2; х₂=-8-√16/2=-6 т.е. (х²+8х+12)/(х+4)²=(х+2)(х+6)/(х+4)², т.к. (х+4)²> 0, нас интересует только знак, поэтому рассматриваем равносильное выражение (х+2)(х+6) ++→х f´(-7)= (-7++6)=-5*(-1)> 0 f´(-5)= (-5++6)=-3*1< 0 f´(-3)= (-3++6)=-1*3< 0 f´(0)= (0+2)(0+6)=2*6> 0 в точке х=-6 производная меняет знак с + на - значит это точка максимума; в точке х=-4 производная не меняет знак ,значит это точка не является точкой экстремума ; в точке х=-2 производная меняет знак с – на +, значит это точка минимума; удачи!
Уравнение параболы y=ax^2+bx+c
Так как парабола проходит через точку А(8;-2), то
-2=64а+8b+c (1)
Координаты вершины параболы (2;4), через неё парабола тоже, логично, проходит, поэтому
4=4а+2b+c (2)
А также абсцисса вершины параболы определяется по формуле
x=-b/2a => 2=-b/2a, 4a=-b,
4a+b=0 (3)
Работаем с выражениями (1), (2) и (3):
(1-2) -6=60а+6b; 36a+6*(4a+b)=-6;
Т.к. 4a-b=0, то 36a=-6; a=-1/6
(3) 4a=-b; 2/3=b
Подставляем найденные значения а и b в выражение (2)
4=-4/6 + 4/6 + с, с=4
Поэтому искомое уравнение параболы
ответ: - 1/6 x^2 + 2/3 x + 4
ответ:-3/5