Выразим у через х:
4у = x^2 - 4x
y = 0,25x^2 - x
Парабола, служащая графиком квадратного трехчлена, обычно задается уравнением y = Ax^2 + Bx + C, где A, B, и C — константы. Ось такой параболы параллельна оси ординат. Координаты вершины параболы равны (-B/2A, - B^2/(4A) + C).
Находим координаты вершины: (2; -1)
Такая парабола полностью эквивалентна параболе, заданной уравнением y = Ax^2, сдвинутой путем параллельного переноса на -B/2A по оси абсцисс и на -B^2/(4A) + C по оси ординат. Это легко проверить заменой координат. Следовательно, если вершина параболы, заданной квадратичной функцией, находится в точке (x, y), то фокус этой параболы находится в точке (x, y + 1/(4A)).
Итак, координаты фокуса: (2; 0)
Всего у нас было 252 голоса. Известно из условия, что голоса распределились в отношении 2:7. Значит наше уравнение будет выглядеть так:
2*Х + 7*Х = 252
(Если бы у тебя было 100 голосов, а распределились бы в отношении 3:4, то уравнение было бы 3*Х + 4*Х = 100
Понятно?)
Итак, вернемся к нашему уравнению:
2*Х + 7*Х = 252
Решаем:
9*Х = 252
Х = 252/9 = 28
Но это вовсе не ответ! Смотрим на вопрос задачи: "Сколько голосов получил проигравший?"
Думаю, понятно, что при отношении 2:7 проиграл первый депутат. Так как к нему относится тут число 2, то домножаем наш Х на 2:
Х*2 = 28*2 = 56
(Если, допустим, отношение было 3:4, а Х уже найден, то кол-во голосов первого равно 3*Х)
ответ: В (56)
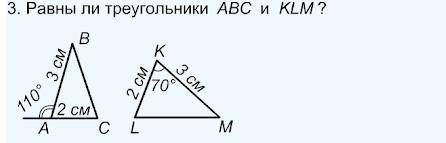
Нет,на глядно даже сравнить можно