3 *5^(2x-1) -2*5^(x-1) = 0.2
3*5^2x* 5^(-1) - 2 *5^x * 5^(-1) - 0.2=0
3/5 * 5^2x - 2/5 * 5^x -0.2=0
5^x= t
3/5 t ² - 2/5 t - 0.2 =0
0.6t² - 0.4t -0.2=0 |:0,2
3t² - 2t - 1 =0
D= 4 - 4*3*(-1) = 4+12 = 16 = 4²
t₁= (2-4) / (2*3) = -2/6 = -1/3
t₂ = (2+4)/6 = 6/6 =1
5^x= - 1/3
5^x = - 3^(-1) - нет вещественных корней
5^x = 1
5^x = 5^0
x=0
2)
3*5^(2x-1)-2*5^(x-1)=0,2
(3/5)*5^(2x)-(2/5)*5^x-0,2=0
5^x=t>0 ⇒
0,6t²-0,4t-0,2=0 I×5
3t²-2t-1-0 D=16
t₁=1 ⇒ 5^x=1 x=0
t₂=-1/3 t₂∉
Объяснение:
7; -4
Объяснение:
Решение методом подбора корней:
Записываем исходное уравнение:
(х - 7)(х + 4) = 0
Подбираем х:
х1 = 7, х2 = -4
Решение через раскрытие скобок, теорему Виета, и дискриминант:
Записываем исходное уравнение:
(х - 7)(х + 4) = 0
Раскрываем скобки:
х*х - 7x + 4x - 28 = 0
x^2 - 7x + 4x - 28 = 0
Приводим подобные:
x^2 - 3x - 28 = 0
1 под
Решаем через теорему Виета:
x1 + x2 = 3
x1*x2 = -28
Откуда:
x1 = 7, x2 = -4
2 под Решение через дискриминант
Записываем исходное уравнение:
x^2 - 3x - 28 = 0
Ищем дискриминант:
D = b^2 - 4ac
D = (-3)^2 -4*1*(-28)
D = 9 - (-112)
D = 9 + 112 = 121
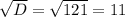
Находим корни уравнения:
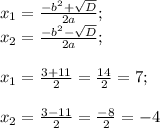
В данном решении показано решения данного уравнения. (причем имеет 2 под
Упростим выражение
cos^2(x)*sin^2(x)=(cosx*sinx)^2= (1/2*sin2x)^2
Значит требуется теперь построить функцию
y=1/4sin^2(2x)