В арифметической прогрессии первый член 10 и разность d . a) Найдите пятый член прогрессии и сумму первых пяти членов прогрессии. [3]
b) Обозначим n-й член прогрессии через an. Найдите наименьшее натуральное число n
такое, что an >170. [3]
3. Сумма трех чисел, представляющих возрастающую арифметическую прогрессию равна 21. Если к ним, соответственно, добавить 2, 3, и 9 то образованные числа составят геометрическую прогрессию. Найти наибольшее из искомых членов прогрессии. [4]
4. Первый, второй и третий члены геометрической прогрессии соответственно равны
2k 8; k; k , где k - положительное число.
а) Найдите значение k .
b) Найдите сумму бесконечно убывающей геометрической прогрессии. [4]
5. Работники получили задание выкопать колодец. За первый выкопанный в глубину метр колодца им платят 2000 тг, а за каждый следующий – на 2000 тг больше, чем за предыдущий. Сколько денег заплатят работникам за выкопанный колодец глубиной 12 м [5]
 км/мин.
км/мин.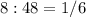 км/мин.
км/мин.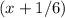 км/мин.
км/мин.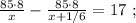
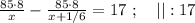
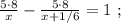
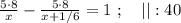
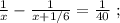
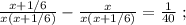
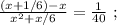
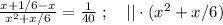
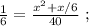
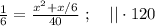
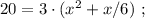
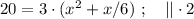
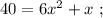
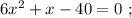
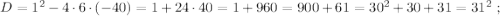
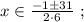
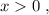 так, как это скорость,
так, как это скорость,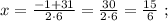
Выразим а2, а4 , а6 через первый член арифметической прогрессии и разность прогрессии (d)
a2=a1+d a4=a1+3d a6=a1+5d и подставим в систему:
{a1+a1+5d=11 a1+d+a1+3d=10
{2a1+5d=11 2a1+4d=10
Решим систему методом сложения. Умножим первое уравнение на (-1) и сложим со вторым:
{-2a1-5d=-11 + 2a1+4d=10
-d=-1
d=1
2a1+4=10
a1=3 (подставили найденное значение d во второе уравнение системы и нашли первый член прогрессии.)
По формуле суммы n-первых членов прогрессии найдём сумму первых шести членов этой прогрессии:
S6=(2·3+5 )\2·6=33 (Sn=(2a1+d(n-1))\2·n)
ответ:33