Чтобы изобразить график линейной функции вида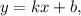 
где 
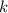и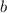 
— коэффициенты, достаточно на координатной плоскости отметить две точки и провести через них прямую.
Для этого строят таблицу для двух точек: первая строка — абсцисса (иксы), вторая строка — ордината (игреки). Вы — хозяин своей таблицы. Подбирайте любое значение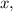 
подставляйте его в функцию и находите 
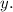(Подбирайте числа в пределах разумного.)
Пример. Изобразить график линейной функции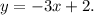 
Строим таблицу для двух точек:
Пусть 
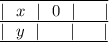
Тогда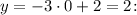 
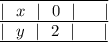
Пусть 
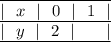
Тогда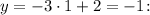 
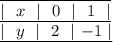
Имеем заполненную таблицу для двух точек. Изобразим координатную плоскость, отметим две точк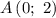и: 
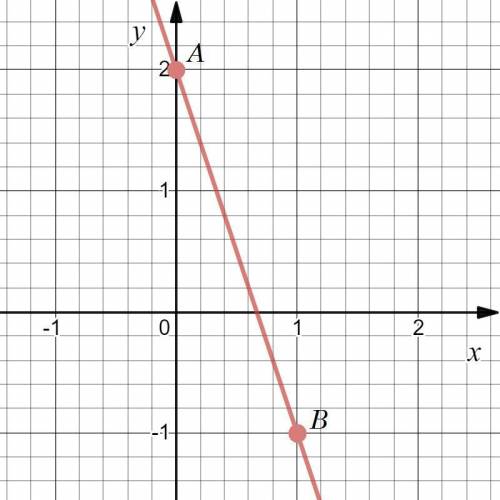
и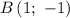 
— и проведем через них прямую (см. вложение). График линейной функции 
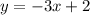построен.
1) рассмотрим сначала первый корень:
1.1 распишем синус двойного угла, вынесем 4 за скобки
1.2 единицу распишем по основному тригонометрическому тождеству как 1 = sin²a + cos²a
1.3 в скобках можно собрать формулу (а - б)² = а² + б² - 2аб
1.4 помним о том, что корень извлекается по модулю
1.5 так как по условию дано, что угол находится в 4 четверти, в которой синус отрицательный, а косинус положительный, то раскрываем модуль со знаком плюс
2) рассмотрим второй корень:
2.1 вынесем 2 за скобки и распишем косинус двойного угла
2.2 единицу распишем по основному тригонометрическому тождеству и приведем подобные слагаемые
2.3 корень извлекается по модулю, косинус раскрываем с +
3) переписываем то, что получилось, приводим подобные слагаемые
Объяснение:
y=4x³ -9x² +6x
все ищем через производную
y'(х₀) =0 это и будут точки экстремумов
y' = 12x²-18x+6
12x²-18x+6 = 0 ⇒ х₁=1; х₂= 0,5;
у(1) = 1
у(0,5) = 1,25
чтобы определить минимум или максимум берут вторую производную (хотя здесь и так видно, что х₁=1 это точка минимума, а х₂= 0,5 точка максимума.
но проверим, как положено
y'' = 24x-18
y''(1) = 6>0 - значит точка x₁= 1 точка минимума функции.
y''(0,5) = -6< = значит точка х₂= 0,5 - точка максимума функции.