Графиком уравнения в любом случае будет прямая. Она не будет пересекать ось ординат только в том случае, если сама прямая будет параллельна ей.
В свою очередь прямая, параллельная оси ординат, имеет вид  , где
, где  - какое-либо число. Заметим что здесь вообще не переменной
- какое-либо число. Заметим что здесь вообще не переменной 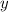 .
.
Можно сделать вывод, что график не будет пересекать ось ординат тогда и только тогда, когда коэффициент перед 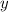 - это
- это 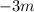 - равен 0.
- равен 0.
Т.е. 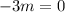 , откуда
, откуда 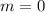 .
.
Можем сделать проверку: подставляем 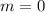 в уравнение.
в уравнение.
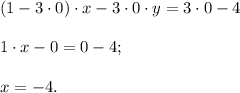
т.е. в итоге получили прямую, параллельную оси ординат.
ОТВЕТ: 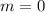
Коэффициент подобия по определению считается по линейным размерам .
Для периметра (сумме линейных размеров) он равен k, для площадей k^2,
для объемов k^3.Тогда периметр равен 12*4=48 см, площадь равна 9*4^2=144 кв. см
Как-то так
Объяснение:
<!--c-->
Отношение периметров двух подобных треугольников равно коэффициенту подобия.
P(ABC)P(RTG)=k20P(RTG)=19P(RTG)=9⋅20=180(см)
Отношение площадей двух подобных треугольников равно квадрату коэффициента подобия.
S(ABC)S(RTG)=k26S(RTG)=(19)26S(RTG)=181S(RTG)=6⋅81=486(см2)