Указанное разложение невозможно.
Объяснение:
Разложим число 91 на простые множители:
91 = 7•13.
Делители числа 91: 1, 7, 13, 91.
Других натуральных делителей нет. Никакие два из них на 5 не отличаются. Задача решений не имеет.
Второй
Обозначим меньший натуральный множитель за х, тогда второй по условию равен (х+5).
Зная, что произведение множителей равно 91, составим и решим уравнение:
х•(х + 5) = 91
х² + 5х - 91 = 0
D = 25 + 364 = 389
x1 = (-5+√389)/2 - иррациональное, не является натуральным числом.
х2 = (-5-√389)/2 - отрицательное, не является натуральным числом.
Задача решения не имеет.
Решить систему уравнений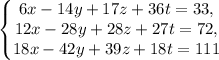
и выделить общее решение соответствующей однородной системы и частное решение неоднородной.
Решение. Выпишем расширенную матрицу системы и будем выполнять элементарные преобразования строк данной матрицы.
Вычислим ранг данной матрицы: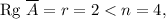
где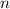 
- число неизвестных. Система имеет нетривиальные решения. Базисный минор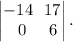 
Ставим в соответствие расширенной матрице упрощенную систему:
где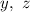
- базисные переменные, 
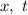- свободные переменные.
Положив значения свободных переменных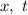
равными нулю, получим частное решение неоднородной системы: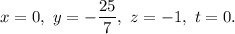 
Общее решение: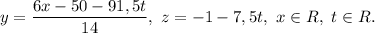
ответ: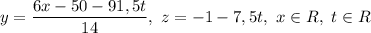
- общее решение; 
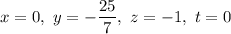- частное решение.