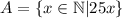
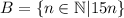
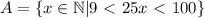
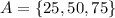
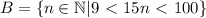
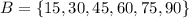
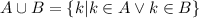- то есть, это такое множество всех k, так что, либо k в А либо в В, или в А и в В одновременно.
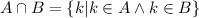- то есть, это такое множество всех k, так что, k и в А и в В одновременно.
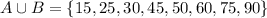- то есть, это множество всех чисел которые кратны либо 25 либо 15, или 25 и 15 одновременно.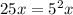
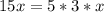
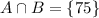
27-8a^3=3^3-(2a)^3=(3-2a)(9+6a+4a^2)
8x^3+y^3=(2x)^3+y^3=(2x+y)(4x^2-2xy+y^2)
27a^3-8b^3=(3a)^3-(2b)^3=(3a-2b)(9a^2+6ab+4b^2)
1+64y^3=1^3+(4y)^3=(1+4y)(1-4y+16y^2)