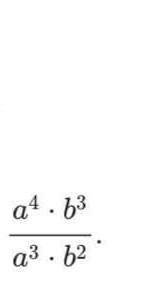
1) Представляем в виде многочлена математическое выражение:
1. (с - 6)² = (с - 6)(с - 6) = с² - 6с - 6с + 36 = с² - 12с + 36;
2. (2а - 3в)² = (2а - 3в)(2а - 3в) = 4а² - 6ав - 6ав + 9в² = 4а² - 12ав + 9в²;
3. (5 - а)(5 + а) = 25 + 5а - 5а - а² = 25 - а²;
4. (7х + 10у)(10у - 7х) = 70ху - 49х² + 100у² - 70ху = 100у² - 49х²;
2) Раскладываем на множители:
1. в² - 49 = в² - 7²;
2. с² - 8с + 16 = (с - 4)(с - 4) = (с - 4)²;
3. 100 - 9х² = 10² - (3х)²;
4. 4а² + 20ав + 25в² = (2а)² + 5в(4а + 5в);
3) Максимально возможно упрощаем выражение:
(х - 2)(х + 2) - (х - 5)² = (х - 2)(х + 2) - (х - 5)(х - 5) = (х² + 2х - 2х - 4) - (х² - 5х - 5х + 25) =
х² - 4 - х² + 10х - 25 = 10х - 29;
4) Решаем уравнение с одним неизвестным:
4(3у + 1)² - 27 = (4у + 9)(4у - 9) + 2(5у + 2)(2у - 7);
4(3у + 1)(3у + 1) - 27 = (4у + 9)(4у - 9) + 2(5у + 2)(2у - 7);
Раскрываем скобки:
4(9у² + 3у + 3у + 1) - 27 = (16у² - 36у + 36у - 81) + 2(10у² - 35у + 4у - 14);
4(9у² + 6у + 1) - 27 = (16у² - 81) + 2(10у² - 31у - 14);
36у² + 24у + 4 - 27 = 16у² - 81 + 20у² - 62у - 28;
Приводим подобные:
36у² + 24у - 23 = 36у² - 62у - 109;
Переносим с противоположным знаком известное в правую часть равенства, неизвестные в левую:
36у² + 24у - 36у² + 62у = 23 - 109;
И снова приводим подобные:
86у = - 86;
Делим обе части равенства на коэффициент при у:
у = - 86 / 86;
у = - 1;
Проверяем:
4(3 х (- 1) + 1)² - 27 = (4 х (- 1) + 9)(4 х (- 1) - 9) + 2(5 х (- 1) + 2)(2 х (- 1) - 7);
4(- 3 + 1)² - 27 = (- 4 + 9)(- 4 - 9) + 2(- 5 + 2)(- 2 - 7);
4 х 4 - 27 = 5 х (- 13) + 2 х (- 3) х (- 9);
16 - 27 = - 65 + 54;
- 11 = - 11.