1. [ ] Преобразуйте уравнение (х + 7)2 - 4х = 2х(х - 5) к виду ax2 + bx + c = 0. Укажите старший коэффициент, второй коэффициент и свободный член этого уравнения.
2. а) [ ] Определите, какое из уравнений является неприведенным квадратным уравнением и найдите его корни: А) 3x2 − 2x - 5 = 0; В) x2 + 6 x - 9 = 0; С) x2 + 7x - 8 = 0; D) x2 − 3x + 9 = 0
б) [ ] Составьте приведенное квадратное уравнение, имеющие корни
х1= 8, х2 = – 2.
3. [ ] Дано квадратное уравнение 2х2 - 16х + с = 0.
а) Определите, при каких значениях параметра с уравнение имеет два одинаковых корня.
б) Найдите эти корни уравнения.
4. [ ] Для квадратного трехчлена х2 – 10х + 21
а) выделите полный квадрат;
б) разложите квадратный трехчлен на множители
4. [ ] Не вычисляя корней квадратного уравнения х2 + 8х - 65 = 0, найдите
а) Укажите область допустимых значений уравнения;
б) Приведите рациональное уравнение к квадратному уравнению;
в) Найдите решения рационального уравнения.
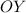 равна
равна 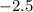 , когда
, когда 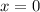 , то есть эти точка должны пересекаться в этих точках .
, то есть эти точка должны пересекаться в этих точках . 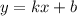 то вторая
то вторая 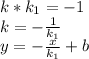
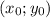 это есть точка касательной к графику то у второй
это есть точка касательной к графику то у второй 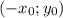 .
. 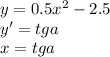
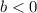 так как график сам расположен ниже оси
так как график сам расположен ниже оси 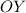
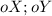 , он прямоугольный по условию прямые перпендикулярные , пользуясь запись уравнения прямых получаем что они делятся на равные углы по
, он прямоугольный по условию прямые перпендикулярные , пользуясь запись уравнения прямых получаем что они делятся на равные углы по 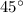
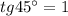
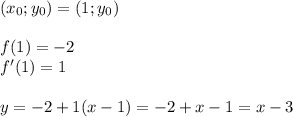
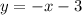
1. Преобразуйте уравнение (х + 7)2 - 4х = 2х(х - 5) к виду ax2 + bx + c = 0. Укажите старший коэффициент, второй коэффициент и свободный член этого уравнения.
Переобразуем:
Переносим в общую сторону (левую) и меняем знаки:
Сокрашаем:
ответ:
Старший коэффициент: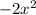
Второй коэффициент: 8x
Свободный член: -14
2. а) Определите, какое из уравнений является неприведенным квадратным уравнением и найдите его корни:
А)
В)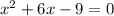
С)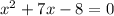
D)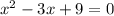
У неприведенных квадратных уравнениях, старшие коэффициенты не равны 1. (0/5, 3, 5, -17, тд - все неприведенные квадратные уравнения).
A)
2. б) Составьте приведенное квадратное уравнение, имеющие корни х1= 8, х2 = –2.
По теореме Виета:
ответ:
3. Дано квадратное уравнение 2х^2 - 16х + с = 0.
а) Определите, при каких значениях параметра с уравнение имеет два одинаковых корня.
Если дискриминант (D) квадратного уравнения равен 0, то уравнение имеет 1 корень, или говорят и
и 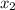 совпадают.
совпадают.
Если p = 0, то
ответ: c = 32
3. б) Найдите эти корни уравнения
ответ:
Дальше не знаю как решать