
ответ: x^3 + 2*x^2 + 4*x + 8
Объяснение: Пускай a, b, c, d - коэффициенты. Тогда:
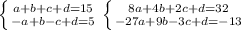
Система из 4 линейных уравнений с 4 неизвестными - решение можно найти и оно только одно. Решаем систему либо методом Гаусса, либо методом обратной матрицы, либо другими известными. Вот пример через Гаусса:
a+b+c+d = 15 => d = 15-a-b-c
-a+b-c+d = 5 => -a+b-c+15-a-b-c = 5 => -2a-2c= -10 => c = 5-a
8a+4b+2c+d=32 => 8a+4b+10-2a+15-a-b-5+a=32 => 6a+3b=12 => b = 4-2a
-27a+9b-3c+d=-13 => -27a +36-18a-15+3a+15-a-4+2a-5+a=-13 => -40a = -40 => a = 1
Из этого находим другие коэффициенты.
1.
А) (1,075-0,05):0,25=1.025:0,25=4,1
Б) 3/5:5/6+2,5*0,4-1:1 1/9=3/5*6/5+1-1:1 1/9 =18/25+1-1 1/9=1 18/25 - 1 1/9= 43/25-10/9=387/225-250/225=(387-250)/225=137/225
В) (-2)³+(1/2)² * 2⁴=-8+0,25 * 16=-8+4=-4
Г)слишком сложно
2.
А)2 1/8 = 17/8=17:8=2,125
Б)30/13 = 30:13=2,307...