Дано квадратное уравнение: 4х2 – 8х + с = 0. а) При каких значенияхпараметра с данное уравнение имеет два одинаковых действительных корня? б) Найдите эти корни.
1. Всего карточек 50 из них 9; 18; 27; 36; 45 кратны 9 - их всего 5 карточек.
Всего все возможных событий: n=50
Всего благоприятных событий: m = 5
Искомая вероятность: P = m/n = 5/50 = 1/10 = 0,1.
2. Всего все возможных подбрасывания игральных кубиков: 6*6=36
На желтой кости выпало четное число: {2;4;6}
На красной кости - {5}
Всего благоприятных событий: 3*1 = 3.
Искомая вероятность: P = 3/36 = 1/12
3. Вероятность того, что вынутая наугад карта окажется шестеркой красной масти равна . Тогда вероятность того, что вынутая наугад карта окажется не шестеркой красной масти равна
4. Выпишем все выпадения очков, в сумме не меньше 11.
{6;6}, {5;6}, {6;5} - всего 3
Искомая вероятность: P = 3/36 = 1/12
5. Всего все возможных событий:
Один красный шар можно достать а один белый По правилу произведения, достать один красный и один белый шары можно
Поскольку переменная х входит в чётной степени, то график заданной функции симметричен относительно оси у. Производная этой функции равна нулю пр х = 0. Подставив это значение в уравнение функции, получаем у = 1. Исследуем поведение производной вблизи точки х = 0. х 0.5 0 -0.5 у' -0.6875 0 0.6875. Производная переходит с + на -, значит, при х = 0 имеем максимум функции, равный у = 1. Минимальное значение на заданном отрезке найдём, подставив значение х = +-3 в уравнение (достаточно х = 3, так как функция чётная) ymin = 1-3⁴-3⁶ = 1-3⁴*(1+3²) = 1-81*(1+9) = 1-810 = -809. ответ при (х=+-3) : умакс = 1, умин = -809.
1. Всего карточек 50 из них 9; 18; 27; 36; 45 кратны 9 - их всего 5 карточек.
Всего все возможных событий: n=50
Всего благоприятных событий: m = 5
Искомая вероятность: P = m/n = 5/50 = 1/10 = 0,1.
2. Всего все возможных подбрасывания игральных кубиков: 6*6=36
На желтой кости выпало четное число: {2;4;6}
На красной кости - {5}
Всего благоприятных событий: 3*1 = 3.
Искомая вероятность: P = 3/36 = 1/12
3. Вероятность того, что вынутая наугад карта окажется шестеркой красной масти равна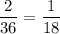
. Тогда вероятность того, что вынутая наугад карта окажется не шестеркой красной масти равна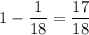 
4. Выпишем все выпадения очков, в сумме не меньше 11.
{6;6}, {5;6}, {6;5} - всего 3
Искомая вероятность: P = 3/36 = 1/12
5. Всего все возможных событий: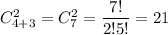
Один красный шар можно достать а один белый По правилу произведения, достать один красный и один белый шары можно
Искомая вероятность: P = 12/21 = 4/7