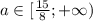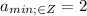Можно ли в четырехугольник со сторонами 3; 2; 1; 5 вписать окружность?

👇

Ответ:

Grinberg2003

10.04.2020

Нельзя,т.к. по теореме о описанном около окружности 4-угольнике противоположные стороны должны быть равны.а 3+2+1+5=11 следовательно сумма прот.сторон должна быть равна 5,5 что противоречит геометрическому смыслу.чтд

4,6(24 оценок)

Открыть все ответы

Ответ:

Marina4578

10.04.2020

30% числа k = 0,3a

35% числа p = 0,35p

0,3k > 0,35p на 20

Первое уравнение:

0,3k - 0,35p = 20

20% числа k = 0,2а

30% числа p = 0,3р

0,3р > 0,2k на 8

Второе уравнение:

0,2k + 8 = 0,3p

Решаем систему.

{0,3k-0,35р = 20

{0,2k - 0,3р = - 8

Первое умножим на 2, а второе умножим на (-3)

{0,6k-0,7р = 40

{-0,6k+0,9р = 24

Сложим

0,6k-0,7р -0,6k+0,9р = 40+24

0,2р = 64

р = 64 : 0,2

р = 320

В первое уравнение 0,3k - 0,35p = 20 подставим р = 320.

0,3k - 0,35·320 = 20

0,3k - 112 = 20

0,3k = 112 + 20

0,3k = 132

k = 132 : 0,3

k = 440

ответ: k = 440;

р = 320.

4,7(81 оценок)

Ответ:

Bananchik26

10.04.2020

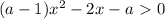
$(a-1)x^2-2x-a\ \textgreater \ 0$
Если a=1

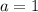, то получим линейное неравенство: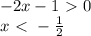
$-2x-1\ \textgreater \ 0
\\\
x\ \textless \ - \frac{1}{2}$
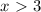Полученный промежуток не включает в себя заданыый $x\ \textgreater \ 3$ .
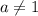Рассматриваем случай, когда $a \neq 1$ - имеем квадратное неравенство.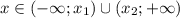
Заданное неравенство ">0", в зависимости от знака старшего коэффициента общие решения неравенства можно записать в виде:
- если старший коэффициент больше 0: $x\in(-\infty;x_1)\cup(x_2;+\infty)$
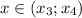
- если старший коэффициент меньше 0: $x\in (x_3;x_4)$
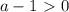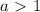
Вывод: необходимо рассмотреть случай с положительным старшим коэффициентом: $a-1\ \textgreater \ 0$ , тогда $a\ \textgreater \ 1$
Решаем неравенство. Приравниваем левую часть к нулю:
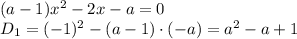
$(a-1)x^2-2x-a=0
\\\
D_1=(-1)^2-(a-1)\cdot(-a)=a^2-a+1$
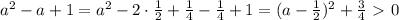
Получившийся дискриминант всегда больше 0, т.к. $a^2-a+1=a^2-2\cdot \frac{1}{2} + \frac{1}{4} - \frac{1}{4} +1=(a- \frac{1}{2} )^2+ \frac{3}{4}\ \textgreater \ 0
$
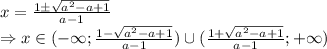
$x= \frac{1\pm \sqrt{a^2-a+1} }{a-1} 
\\\
\Rightarrow x\in(-\infty; \frac{1-\sqrt{a^2-a+1} }{a-1} )\cup( \frac{1+\sqrt{a^2-a+1} }{a-1} ;+\infty)$
Чтобы получившийся ответ включал интервал х>3, необходимо потребовать выполнение следующего условия:
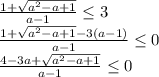
$\frac{1+\sqrt{a^2-a+1} }{a-1} \leq 3
\\\
 \frac{1+\sqrt{a^2-a+1} -3(a-1)}{a-1} \leq 0
\\\
 \frac{4-3a+\sqrt{a^2-a+1} }{a-1} \leq 0$
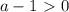Так как в рассматриваемом случае $a-1\ \textgreater \ 0$ , то можно перейти к следующему неравенству:
$4-3a+\sqrt{a^2-a+1} \leq 0
\\\
\sqrt{a^2-a+1} \leq 3a-4
\\\
\begin{cases} a^2-a+1 \leq (3a-4)^2 \\ 3a-4\ \textgreater \ 0 \right \end{cases}
\\\
\begin{cases} a^2-a+1 \leq 9a^2-24a+16 \\ 3a\ \textgreater \ 4 \right \end{cases}
\\\
\begin{cases} 8a^2-23a+15 \geq 0 \\ a\ \textgreater \ \frac{4}{3} \right \end{cases}
\\\
\begin{cases} a\in(-\infty;1]\cup[ \frac{15}{8} ;+\infty) \\ a\ \textgreater \ \frac{4}{3} \right \end{cases}$
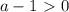Итоговое решение с учетом рассматриваемого ограничения $a-1\ \textgreater \ 0$ : $a\in[ \frac{15}{8} ;+\infty)$
Искомое минимальное целое значение $a_{min; \in Z}=2$
ответ: 2

4,7(51 оценок)

Это интересно:

Компьютеры-и-электроника

14.08.2022

Как поставить пароль на Google Chrome: простое решение для защиты вашей конфиденциальной информации...

Финансы-и-бизнес

16.02.2020

Как прекратить арендный контракт: шаг за шагом...

Семейная-жизнь

29.04.2022

Как выявить ранние признаки беременности...

Питомцы-и-животные