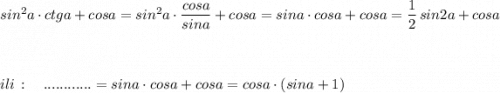
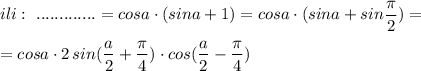
В решении.
Объяснение:
Задание 1.
Известно, что график функции f(x) проходит через точку (−5; 3) и параллелен графику функции y = −4x + 3.
а) Найдите уравнение данной функции f(x) ( ).
Графики линейных функций параллельны, если k₁ = k₂, а b₁ ≠ b₂.
k₁ = -4, значит, k₂ = -4;
Вычислить b₂:
Подставить в уравнение известные значения х и у (координаты точки) и вычислить b₂:
3 = -4 * (- 5) + b₂:
3 = 20 + b₂:
3 - 20 = b₂:
b₂ = -17;
Уравнение второй функции:
у = -4х - 17.
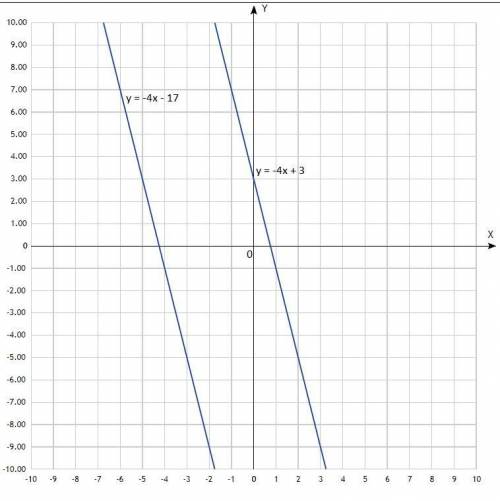
б) Постройте график данной функции f(x) ( ).
Построить графики. Графики линейной функции, прямые линии. Придать значения х, подставить в уравнение, вычислить у, записать в таблицу. Для построения прямой достаточно двух точек, для точности построения определить три.
y = −4x + 3 у = -4х - 17
Таблицы:
х -1 0 1 х -6 -5 -4
у 7 3 -1 у 7 3 -1
По вычисленным точкам построить графики.
Дана система ур-ний 2x−y=19x−2 5y=14 Приведём систему ур-ний к каноническому виду −17x−y=−2 5y=14 Запишем систему линейных ур-ний в матричном виде [−17−1−20514] В 1 ом столбце [−170] делаем так, чтобы все элементы, кроме 1 го элемента равнялись нулю. - Для этого берём 1 ую строку [−17−1−2] , и будем вычитать ее из других строк: Во 2 ом столбце [−15] делаем так, чтобы все элементы, кроме 2 го элемента равнялись нулю. - Для этого берём 2 ую строку [0514] , и будем вычитать ее из других строк: Из 1 ой строки вычитаем: [−17−0−1−−1−2−−145]=[−17045] получаем [−170450514] Все почти готово - осталось только найти неизвестные, решая элементарные ур-ния: −17x1−45=0 5x2−14=0 Получаем ответ: x1=−485 x2=145
Объяснение: