D)-5a^2b^3
вот решение на фотографии...

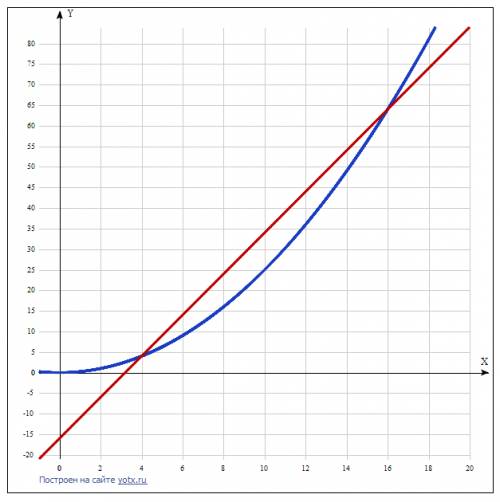
 . Графиком данной функции является парабола, ветви которой направлены вверх. Следовательно, минимальное значение функции соответствует вершине параболы.
. Графиком данной функции является парабола, ветви которой направлены вверх. Следовательно, минимальное значение функции соответствует вершине параболы.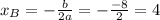
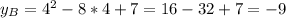
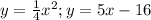
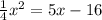
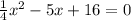
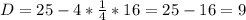
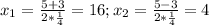
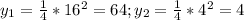
ответ
1) 12a2ba – 2abab2 + 11aba = 12a3b – 2a2b3 + 11a2b
2) 2ab2 4ab – 3a28aba – 2abab2 = 8a2b3 – 24a4b + 2a2b3
3) 1,5xy2(-4)xyz – 4mnk5m2nk = -6x2y3z – 20m3n2k2
4) 4cc2c • (- 1/4) bc + 5xy2xy2 = - c5b + 5x2y4
Объяснение: