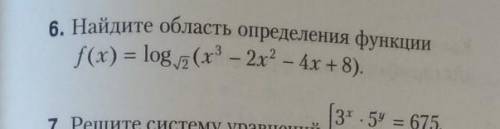
Объяснение: x^3-2x^2-4x+8>0,
x^2(x-2)-4(x-2)>0, (x-2)*(x^2-4)>0, (x-2)^2 *(x+2)>0
- - - - - - - -(-2) + + + + + + (2) + + + + + + , отв. (-2;2) и (2; + бескон.),
методом интервалов
Cгруппируем слагаемые и используя формулу суммы кубов
а³+в³=(а+в)(а²-ав+в²), разложим на множители левую часть уравнения.
(x³+8)-(3x²+6x)=0; (х+2)(х²-2х+4)-3х*(х+2) =0;
(x+2)(x²-2x+4-3x)=0;
(x+2)(x²-5x+4)=0;
x+2=0; х=-2 или х²-5х+4=0 , ДЛЯ последнего УРАВНЕНИЯ
x₁·x₂=4
x₁+x₂=5, теперь просто подберите два числа, чтобы если их сложить, получить второй коэффициент, но с противоположным знаком, т.е. 5, а если перемножить, то получить свободный член с тем же знаком,т.е. 4, ясно, что это 1 и 4, т.к. 1+4=5; 1*4=4
ответ 1; 4; -2.
Объяснение:
Достаточно потребовать чтобы многочлен был >0