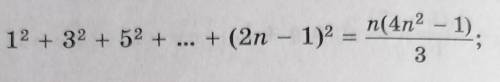
Объяснение:
база индукции n=1
1^2 = 3/3 1=1
шаг индукции
предположим это верно для k
докажем это для k+1
1^2+3^2+...+ (2k-1)^2 + (2(k+1)-1)^2= (k+1)(4(k+1)^2-1) / 3
заметим, что вся вот эта часть над полоской равна k(4k^2-1)/3 прям как в условии
получается
k(4k^2-1)/3+ (2(k+1)-1)^2 = (k+1)(4(k+1)^2-1) / 3
домножаем на 3
k(4k^2-1)+ 3(2(k+1)-1)^2 = (k+1)(4(k+1)^2-1)
теперь просто раскрываем скобки и убеждаемся, что они равны друг другу, значит мы доказали для k+1, а по предположению индукции, доказали для всех k, ну и для n, вообще без разницы
4k^3-k + 12k^2+12k+3 = (k+1)(4k^2+ 8k + 3)
4k^3 + 12k^2 + 11k + 3 = 4k^3 + 12k^2 + 11k + 3
индукция клёвая вещь, легко можно доказывать, что такие вот ряды равны простой формуле (:
запомни этот алгоритм, и сможешь решить любую подобную задачу
доказано
Объяснение:
смотри прикреплённое изображение
доказываем, что выражение верно для n=1, n = 2, ...
Предполагаем, что выражение верно для n = k и доказываем (основываясь на данном предположении), что выражение также верно для n=k+1
В результате успешного данного доказательства можно утверждать, что выражение верно для любого n