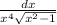
![\int \dfrac{dx}{x^4\sqrt{x^2-1}}=\Big[\ x=\dfrac{1}{cost}\ ,\ dx=\dfrac{sint\, dt}{cos^2t}\ ,\ x^2-1=\dfrac{1}{cos^2t}-1=tg^2t\ \Big]=\\\\\\=\int \dfrac{sint\, dt}{cos^2t\cdot tgt}=\int \dfrac{sint\cdot cost\, dt}{cos^2t\cdot \dfrac{1}{cos^4t}\cdot sint}=\int cos^3t\, dt=\int cos^2t\cdot cost\, dt=\\\\\\=\int (1-sin^2t)\cdot cost\, dt=\Big[\ u=sint\ ,\ du=cost\, dt\ \Big]=\int (1-u^2)\, du=\\\\\\=\int du-\int u^2\, du=u-\dfrac{u^3}{3}+C=sint-\dfrac{sin^3t}{3}+C=](/tpl/images/1615/6309/0849f.png)
Общий вид решения уравнения sin x = a, где | a | ≤ 1, определяется формулой:
x = (- 1)^k · arcsin(a) + πk, k ∈ Z (целые числа),
x = +-arc sin (1/4) + πk ≈ +- 0,25268 + πk, k ∈ Z.Общий вид решения уравнения tg x = a определяется формулой:
x = arctg(a) + πk, k ∈ Z (целые числа).
х = 1,107149 + πk, k ∈ Z.1. Сложить два известных угла, результат вычесть из 180 градусов.
2. Вычесть известный угол из 90 градусов; сложить известный угол с 90, результат вычесть из 180 градусов.
3. 82
4. 98
5. Отрезок BH образует со стороной АС угол в 90 градусов.
6. Точка M разделит отрезок АС пополам.
7. Отрезок BE разделит угол В пополам.
8. Углы при основании равны; биссектриса, проведенная к основанию, является медианой и высотой
9. Касательная, проведенная к окружности, перпендикулярна радиусу, проведенному к точке касания; из любой точки, лежащей вне окружности, можно провести ровно две касательные к окружности; отрезок, соединяющий точку, лежащую вне окружности, с центром окружности, является биссектрисой угла между касательными, проведенными из этой точки к окружности; отрезки касательных (к одной окружности!), проведенных из одной точки, равны.
10. Медианы делятся в отношении 2:1 считая от вершин треугольника.