1.Иван Сергеевич Тургенев ,рассказ "Муму"
2.Очень интересный рассказ, заставляет задуматься
3.Это произведение о немом дворнике Герасиме который переехал работать в Москву, и подобрал себе щенка
Он назвал её Муму, она росла вместе с ним, охраняла двор
Но потом барыня приказала избавиться от собаки
Герасим утопил собаку и уехал обратно в деревню
4.Мне очень понравилась Татьяна
Эта была прачка в доме, ей было 28 лет
Она была маленькая, худая, белокурая
Мне она понравилась за то что она была спокойная, не с кем не заговаривала, только делала свою работу
5.Он хотел показать что мы не должны быть капризны как была барыня
Мы должны быть добрыми, с душой и относиться ко всем с пониманием и любовью если это возможно. И ни в коем случае не предавать, ведь в конце Герасим утопил бедную Муму
6.Этот рассказ показывает что даже самые хорошие люди могут совершить ошибку, у него была душа, он очень любил эту собаку, но ему пришлось её утопить
130см
Объяснение:
Пусть основание = a см, а боковая сторона = b см. Т.к. нам известен периметр, то можем составить одно уравнение - 2a + 2b = 46. Потом нам известно, что боковая сторона больше основание на 3, т.е. b = a + 3
В итоге получается система уравнений, решив ее получим длины a и b:
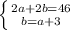
Подставляем в первое уравнение значение b из второго уравнения:
2a + 2(a + 3) = 46
2a + 2a + 6 = 46
4a = 40
a = 10 см
Подставляем значение а во второе уравнение:
b = 10 + 3 = 13 см
Теперь, зная длины сторон, на изи узнать площадь:
a * b = 10 * 13 = 130см
f(x) = 4|x| - x²
1. D(f) = R - симметрична относительно 0.
2. f(-x) = 4|-x| - (-x)² = 4|x| - x² = = f(x),
по определению f(x) - чётнвя.
График чётной функции симметричен относительно оси Оу.
3. Построим часть графика для х ≥ 0, а затем отобразим построенную часть симметрично относительно оси Оу.
f(x) = 4x - x² - квадратичная, графиком является парабола, ветви направлены вниз, т.к. а = - 1, а<0.
х вершины = - b/(2a) = -4/(-2) = 2;
у вершины = 4•2 - 2² = 4;
(2;4) - вершина параболы.
Найдём нули функции:
4x - x² = 0
- х (х - 4) = 0
х = 0 или х = 4
(0;0) и (4;0) - точки пересечения с осью Ох.
Изображение графика смотрите в прикреплённом чертеже.