(см. объяснение)
Объяснение:
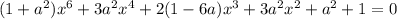
Заметим, что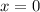 
не является корнем уравнения.
Тогда поделим его на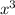 
:
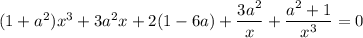
Выполним группировку:
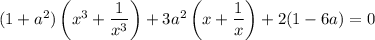
Заметим, что если 
- корень уравнения, то 
тоже.
Тогда единственное решение возможно, если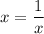 
.
Иными словами, исходное уравнение может иметь ровно один корень тогда, когда 
.
Подставляя 
в исходное уравнение, получаем, что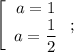 
Подставляя 
, получаем, что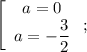 
Теперь решим уравнение при каждом найденном значении параметра и отберем те, при которых имеется единственное решение.
Выполнив необходимые вычисления, получаем, что каждое значение параметра подходит.
Итого при 
исходное уравнение имеет единственное решение.
Задание выполнено!
1. да
2. нет
3. да
4. да
5. нет
6. нет
7. нет
8. нет
9.нет
Объяснение:
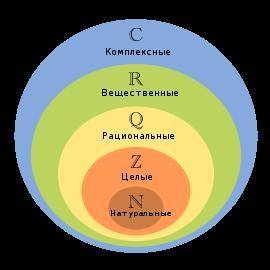
Натуральные числа
Это числа, которые используются при счете: 1, 2, 3... и т.д.
Ноль не является натуральным.
Натуральные числа принято обозначать символом N.
Целые числа. Положительные и отрицательные числа
Натуральные числа, противоположные им и ноль называют целыми числами. Множество целых чисел обозначают символом Z.
Рациональные числа
Это конечные дроби и бесконечные периодические дроби . Множество рациональных чисел обозначается Q. Все целые числа являются рациональными.
Иррациональные числа
Бесконечная непериодическая дробь называется иррациональным числом.
Множество иррациональных чисел обозначается J.
Действительные числа
Множество всех рациональных и всех иррациональных чисел называется множеством действительных (вещественных) чисел.
Действительные числа обозначаются символом R.
Объяснение:
Пусть числа будут х и у. ⇒
ответ: 9.