Объяснение:
1. Найдите значение линейной функцию y=-0,3x+5, если значение аргумента равно 2
x=2
у=0,3*2+5=5,6
2. функция задана формулой y=2x-8. Найдите значение x, при котором y=6.
2х-8=6
2х=14
х=14
3. Лежит ли точка A(-1;2) на графике функции y=5x+7?
Для проверки принадлежит ли точка графику подставим значение точки в функцию.
2=5*(-1)+7
2=2 - точка A(-1;2) принадлежит графику
4. не выполняя построений найдите абсциссу точки пересечения графиков линейных функций: y=3x и y=2x-5
Т.к. графики пересекаются 3х=2х-5
3х-2х=-5
х=-5 абсцисса точки пересечения
5. пусть x и 5 длины сторон прямоугольника в метрах выразите формулой зависимость площади S прямоугольника от переменной x
Формула прямоугольника:
S=5x - линейная функция
6. постройте график линейной функции y=0,5x+4 лежит ли на этом графике точка A(-2;6)
6=0,5*(-2)+6
6≠5 ⇒ точка A(-2;6) не принадлежит графику
7. в каких четвертях расположена функция y=-3x+5 чему равны коэффициенты k и b?
k=-3
b=5
Коэффициент при х меньше 0 ⇒ график нахожится в IV и II четверти.
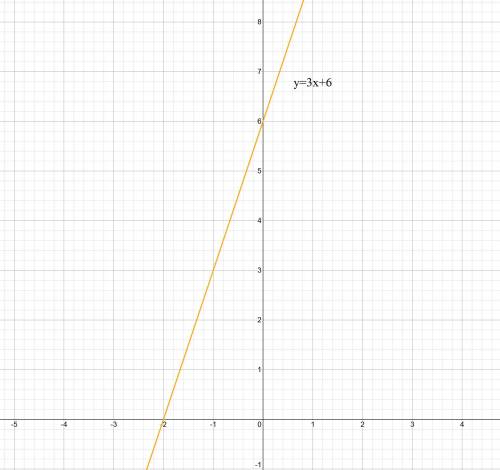
8. построить график функции y=3x+6
Это линейная функция. Построим по 2-м точкам.
х у
0 6
-1 3
Сначала немного теории. Что в данном случае обозначает математическое слово «линейных»? Это значит, что в уравнения системы все переменные входят в первой степени: без всяких причудливых вещей вроде и т.п., от которых в восторге бывают только участники математических олимпиад.
В высшей математике для обозначения переменных используются не только знакомые с детства буквы .
Довольно популярный вариант – переменные с индексами: .
Либо начальные буквы латинского алфавита, маленькие и большие:
Не так уж редко можно встретить греческие буквы: – известные многим «альфа, бета, гамма». А также набор с индексами, скажем, с буквой «мю»:
Использование того или иного набора букв зависит от раздела высшей математики, в котором мы сталкиваемся с системой линейных уравнений. Так, например, в системах линейных уравнений, встречающихся при решении интегралов, дифференциальных уравнений традиционно принято использовать обозначения
Но как бы ни обозначались переменные, принципы, методы и решения системы линейных уравнений от этого не меняются. Таким образом, если Вам встретится что-нибудь страшное типа , не спешите в страхе закрывать задачник, в конце-концов, вместо можно нарисовать солнце, вместо – птичку, а вместо – рожицу (преподавателя). И, как ни смешно, систему линейных уравнений с данными обозначениями тоже можно решить.
Пример 1
Решить систему линейных уравнений:
Здесь у нас дана система из двух уравнений с двумя неизвестными. Обратите внимание, что свободные члены (числа 5 и 7) расположены в левой части уравнения. Вообще говоря, без разницы, где они находятся, слева или справа, просто в задачах по высшей математике нередко они расположены именно так. И такая запись не должна приводить в замешательство, при необходимости систему всегда можно записать «как обычно»: . Не забываем, что при переносе слагаемого из части в часть у него нужно поменять знак.
Что значит решить систему линейных уравнений? Решить систему уравнений – это значит найти множество её решений. Решение системы представляет собой набор значений всех входящих в неё переменных, который обращает КАЖДОЕ уравнение системы в верное равенство. Кроме того, система может быть несовместной (не иметь решений). Не тушуйтесь, это общее определение =) У нас же будет всего лишь одно значение «икс» и одно значение «игрек», которые удовлетворяют каждому уравнению с-мы.
Существует графический метод решения системы, с которым можно ознакомиться на урокеПростейшие задачи с прямой. Там же я рассказал о геометрическом смысле системы двух линейных уравнений с двумя неизвестными. Но сейчас на дворе эра алгебры, и числа-числа, действия-действия.
Решаем: из первого уравнения выразим:
Полученное выражение подставляем во второе уравнение:
Раскрываем скобки, приводим подобные слагаемые и находим значение :
Далее вспоминаем про то, от чего плясали:
Значение нам уже известно, осталось найти:
ответ: x=-4,y=1