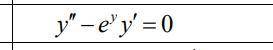
плотность распределения - это производная функции распределения. она равна 0 при х≤1, х>0; и равна
x-1/2 при 1<x≤2
Чтобы найти мат. ожидание. надо найти определенный интеграл от
х*f(dx) от 1 до двух. этот интеграл равен (х³/3-х²/4) от 1 до двух. По формуле Ньютона - Лейбница получаем 8/3-1-(1/3-1/4)=4/3-1/4=13/12
Квадрат мат. ожидания равен 169/144
а дисперсия есть определенный интеграл от 1 до двух от функции х²*f(dx) -М²(х)
интеграл равен х⁴/4-х³/6, подставляем пределы, получаем
4-4/3-(1/4-1/6)=8/3-1/12=31/12, отнимем теперь квадрат мат. ожидания от этой величины и получим дисперсию.
31/12-169/144=(31*12-169)/144=(372-169)/144=203/144=1 59/144
В решении.
Объяснение:
Построить график функции у=х²-2х-3. График - парабола, ветви направлены вверх.
Построить график. Придаём значения х, подставляем в уравнение, вычисляем у, записываем в таблицу.
Таблица:
х -3 -2 -1 0 1 2 3 4 5
у 12 5 0 -3 -4 -3 0 5 12
Значения таблицы указывают на нули функции, точки, в которых парабола пересекает ось Ох, координаты (-1; 0); (3; 0).
Пользуясь графиком, найти:
1)множество решений неравенства х²-2х-3>=0
Смотрим на график. Парабола пересекает ось Ох при х= -1 и х=3.
По графику ясно видно, что у>=0 при значениях х справа и слева от точек пересечения.
Интервал решений неравенства х²-2х-3>=0 х∈(-∞, -1]∪[3, +∞).
Неравенство нестрогое, значения х= -1 и х=3 входят в решения неравенства, скобка квадратная.
2)промежуток убывания функции.
Промежуток убывания функции х∈(-∞, 1).
понижаем порядок: