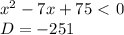
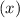, следовательно, корней нет. Чтобы понять это, см. график, который я прикрепил (он здесь: https://www.dropbox.com/sh/hdu5x4aclorg2k3/AAAP31Ze1jlz1RJTpTpHJvd5a?dl=0 — почему-то прикрепляться не хочет). Оранжевым выделены значения, которые нам нужны, а зелёная парабола — это наш график.
В решении.
Объяснение:
Решить систему уравнений:
1) у = 5х + 1
у = 5х - 2
Приравнять правые части (левые равны):
5х + 1 = 5х - 2
5х - 5х = -2 - 1
0 = -3
Система не имеет решений.
2) 2х + 5у + 2 = 0
х + у + 4 = 0
Выразить х через у во втором уравнении, подставить выражение в первое уравнение и вычислить у:
х = -у - 4
2(-у - 4) + 5у = -2
-2у - 8 + 5у = -2
3у = -2 + 8
3у = 6
у = 2;
х = -у - 4
х = -2 - 4
х = -6.
Решение системы уравнений (-6; 2).
Проверка путём подстановки вычисленных значений х и у в систему уравнений показала, что данное решение удовлетворяет данной системе уравнений.
x^2-6xy+9y^2=(x-3y)^2;
|x+2y-4|, (x-3y)^2 >=0, след. |x+2y-4|=(x-3y)^2=0
{ x+2y-4=0; x-3y=0 }
Из второго уравнения x=3y. Подставляем в первое уравнение.
3y+2y-4=0
5y=4
y=4/5
x=12/5
ответ. (12/5, 4/5).