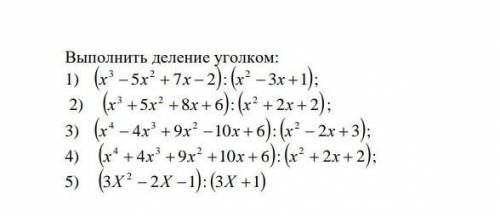
1)х²-64=0
(х-8)*(х+8)=0
а)х-8=0
х=8
б)х+8=0
х=-8
2)4x^2-25=0,раскладываем на множители:
(2х-5)(2х+5)=0
2х-5=0 или 2х+5=0
2х=5 2х=-5
х=2,5
3)9 х2+16=0
х2=-16/9
корней нет, т. к. из отрицательного числа корень нельзя извлечь
4) (2x-3)²-36=0
(2x-3)²=36
2x-3=± 6
2x-3=6 2x=6+3 2x=9 x=9/2
2x-3=-6 2x=-6+3 2x=-3 x=-3/2
ответ:x₁=-3/2
x₂=9/2
ОДЗ: 7-3х≥0
Возводим обе части неравенства в квадрат:
7-3х> 25;
Система:
7-3х≥0;
7-3х >25
равносильна неравенству
7-3х>25;
-3x> 25-7;
-3x > 18;
x< -6.
ответ. (-∞;-6).
2. √(2x+1)>-3
неравенство верно при любом х из ОДЗ.
ОДЗ: 2х+1 ≥ 0
х ≥ -0,5
О т в е т. [-0,5;+∞)
3. √(3+2x)>=√(x+1)
ОДЗ:
3+2х≥0 ⇒ x ≥ -1,5
х+1≥0 ⇒ x ≥-1
ОДЗ: х≥-1
Возводим неравенство в квадрат.
3+2х ≥ х+1;
х ≥ -2
ответ с учетом ОДЗ
х≥ -1
О т в е т. [-1;+∞)
4. √(8-2x)=<√(6x+15)
ОДЗ:
8-2х ≥0 ⇒ х ≤ 4
6х+15≥0 ⇒ х≥-2,5
ОДЗ: - 2,5 ≤ х ≤ 4.
Возводим неравенство в квадрат:
8 - 2х ≤ 6х + 15;
-2х - 6х ≤ 15 - 8
- 8х ≤ 7
х ≥ -7/8
С учетом ОДЗ:
О т в е т. [-7/8;4]