Question

Расстояние между двумя пристанями на реке равно 6 км.катер проплыл это расстояние по течению реки и вернулся обратно 3 часа 45 минут.найдите собственную скорость катера если скорость реки 2 км/ч..буквой x обозначьте собственную скорость катера.

Answer 1

Пусть собственная скорость катера равна х км/ч, тогда скорость катера по течению реки равна (х+2)км/ч, а против течения реки (х-2)км/ч. Так как расстояние между пристанями равно 6 км, то время с которым катер прыл туда равно 6/(х+2), а обратно 6/(х-2). Тогда

6/(х+2)+6/(х-2)=3,45

Answer 2

                                        v                                      t                                         s

По течению - (х+2) км/ч                                 6/(х+2) ч                            6 км

Против течения - (х-2) км/ч                         6/(х-2) ч                               6 км

Скорсть течения - 2 км/ч 

Собст. скорость - х км/ч 

Всего время будет равно 3,75 часа.

Составим и решим уравнение:

$\frac{6}{x+2}+\frac{6}{x-2}-\frac{15}{4}=0 \frac{24(x-2)+24(x+2)-15(x^{2}-4)}{4(x-2)(x+2)}$ 

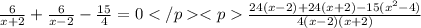
24x-48+24x+48-15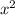$x^{2}$+60=0

48x-15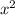$x^{2}$+60=0

15x2-48x-60=0

x$\approx$4,2

4,2(км/ч) - собственная скорость катера.

ответ: 4,2 км/ч.

Не уверен, конечно, что правильно. Скорее всего ты ошиблась в написании задания (условия). Перепроверь и реши по-аналогии.