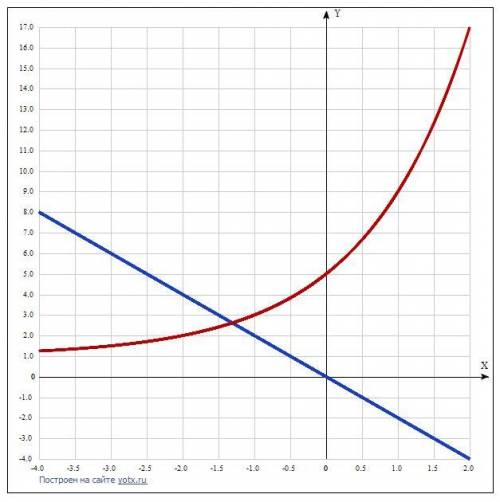
Для графического решения заданное уравнение представим как равенство двух функций: 2^(x + 2) + 1 = -2х.
Точка пересечения их графиков даст корень.
Прямая у = -2х строится по двум точкам, например, х = 0, у = 0.
х = -3, у = 6.
Для построения функции у = (2^(x+2)) + 1 приводит таблицу точек.
x y
-4.0 1.25
-3.5 1.35
-3.0 1.5
-2.5 1.71
-2.0 2
-1.5 2.41
-1.0 3
-0.5 3.83
0 5
0.5 6.66
1.0 9
1.5 12.31
2.0 17.
Точка пересечения х = -1,30785.
Сумма двух последовательных целых чисел, между которыми находится корень уравнения, равна (-2) + (-1) = -3.
Пусть одна сторона (а) земельного участка = x, а сторона, которая больше её на 5км (b) , = x + 5.
Т.к участок имеет прямоугольную форму, будем использовать формулу площади прямоугольника, из которой найдём a и b.
Sпрямоугольника = a * b , где a и b - стороны этого прямоугольника.
Из условия задачи мы знаем, что площадь = 24 км². Стороны = x и x+5 соответственно. Подставим значения в формулу:
24 = x * (x+5)
Раскроем скобки:
24 = x² + 5x
Перенесём 24 в правую сторону с противоположным знаком и приравняем всё выражение к нулю:
x² + 5x - 24 = 0
Решим квадратное уравнение
a(коэффициент у "x²") = 1, b = 5 (коэффициент у "x") , c = -24 ( коэффициент без "x")
D = b² - 4ac = 5²- 4 * 1 * (-24) = 25 + 96 = 121
√D = √121 = 11
x1 = (-b - √D) / 2a = (-5 - 11) / 2 * 1 = -16 / 2 = -8 (a1)
x2 = (-b+√D) / 2a = (-5+11)/ 2 * 1 = 6 / 2 = 3 (a2)
Теперь найдём сторону b:
b1 = x1 + 5 = -8 + 5 = -3
b2 = x2 + 5 = 3 + 5 = 8