Земледелец получает 6,5 кг белокочанной копусты с одного квадратного метра засеянной площади. Для заготовки капусты с кочанов снимаются внешние листья и выпиливаются кочерыжки-при этом теряется 20% массы. Сколько килограммов заготовленной капусты получит земледелец со всех терас своего участка

👇

Увидеть ответ

Ответ:

SASHA123741852

23.04.2022

Объяснение:

Т. к. теряет при заготовке 20%, то остается 80% или 0,8 от первоначальной массы

значит с 1 кв м снимает чистых 6,5 кг/м² * 0,8 = 5,2 кг/м²

соответственно со всех террас заготовит 5,2 кг/м² * 74 м² = 384,8 кг

4,7(33 оценок)

Открыть все ответы

Ответ:

viktpriabihanov

23.04.2022

Объяснение:

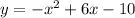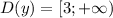
y=-x^2+6x-10 , $D(y)=[3;+\infty)$

данная функция квадратическая, ее график парабола состоит из двух ветвей с общей точкой - вершиной параболы, которые в общем случае делят ее на две подфункции, у каждой из которых своя своя обратная функция

так в базовом виде это для параболы 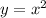y=x^2 вершина (0;0) можно выделить две обратные функции $y=\sqrt{x}; D(y)= [0;+\infty)$ и $y=\sqrt{-x}; D(y)=(-\infty; 0]$

для данной параболы 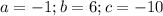a=-1;b=6;c=-10

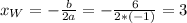
$x_W=-\frac{b}{2a}=-\frac{6}{2*(-1)}=3$

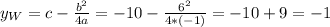
$y_W=c-\frac{b^2}{4a}=-10-\frac{6^2}{4*(-1)}=-10+9=-1$

а значит имеем одну ветвь параболы

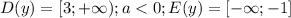
$D(y)=[3;+\infty); a$

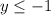( $y \leq -1$ )

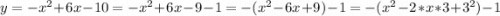
y=-x^2+6x-10=-x^2+6x-9-1=-(x^2-6x+9)-1=-(x^2-2*x*3+3^2)-1

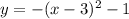
y=-(x-3)^2-1

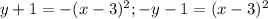
y+1=-(x-3)^2;-y-1=(x-3)^2

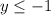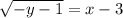
так как $y \leq -1$ : $\sqrt{-y-1}=x-3$

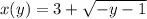$x(y)=3+\sqrt{-y-1}$ --- график тот же что и у исходной функции, но "обратная" зависимость переменных

меняем обозначения (x,y)->(y,x) и получим что

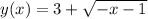$y(x)=3+\sqrt{-x-1}$ , $D(y)=[-\infty; -1]$ А это уравнение обратной функции, график симметричен исходной функции относительно прямой y=x

------------------------------------------------------------------------------------

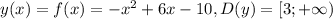
$y(x)=f(x)=-x^2+6x-10, D(y)=[3;+\infty)$

$y(x)=f^{-1} (x)=3+\sqrt{-x-1}, D(y)=[-\infty; -1]$

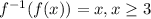
$f^{-1}(f(x))=x, x \geq 3$

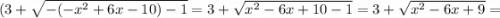
$(3+\sqrt{-(-x^2+6x-10)-1}=3+\sqrt{x^2-6x+10-1}=3+\sqrt{x^2-6x+9}=$

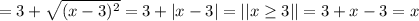
$=3+\sqrt{(x-3)^2}=3+|x-3|=|| x \geq 3 || =3+x-3=x$

аналогично можно убедиться (помним только про области определения и действий функций), что

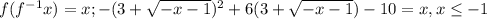
$f(f^{-1}x)=x; -(3+\sqrt{-x-1})^2+6(3+\sqrt{-x-1})-10=x, x \leq -1$

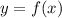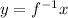!! следует понимать что по факту есть две функции y=f(x) и $y=f^{-1}x$ , x всего лишь условная буква, обозначающая независимый аргумент, y - условная буква, обозначающая значение функции - на их месте могли быть и другие буквы,

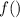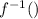более важную роль для понимания обратных функций играет сами f() и $f^{-1} ()$ . (соблюдение взаимно однозначности), а х и y лишь для работы в системе координат XoY

4,6(78 оценок)

Ответ:

annmslna2044

23.04.2022

4320 4380

Объяснение:

номер Гриши, который начинается на 43 и делится на 3, на 4 и на 5.

1.Т.к. номер Гриши делится на 5, то он оканчивается 5 или 0.

2.Т.к. номер Гриши делится на 4, то это чётное число , и значит, он не может оканчиваться 5, следовательно на конце -0.

3. Число делится на 3, если сумма его цифр делится на 3.

Мы знаем 3 цифры номера 4, 3, 0 . Их сумма 4+3+0=7

7+ 2 ÷ 3

7+ 5 ÷ 3

7+ 8 ÷ 3

Значит, на третьем месте могут стоять 3 цифры 2, 5, 8

4320

4350

4380

4. Проверяем признак делимости на 4. Число делится на 4, если его запись оканчивается двумя цифрами, образующими число, которое делится на 4. Остаётся 2 числа

4320 4380

4,6(45 оценок)

Это интересно:

Компьютеры-и-электроника

09.03.2021

Изучаем, как создать общедоступный календарь в Outlook...

Компьютеры-и-электроника

08.05.2020

Как получить очки отряда в Call of Duty Ghosts?...

Образование-и-коммуникации

29.04.2023

Как создать комиксы в стиле Манга...