Определения к заданию
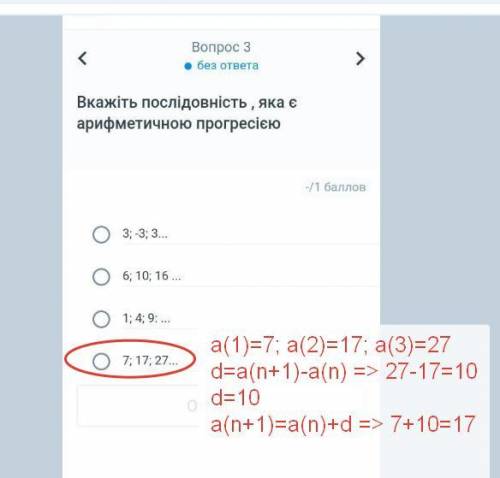
1 )Арифметическая прогрессия - это числовая последовательность, в которой каждый член, начиная со второго, равен сумме первого члена и разности d: a(n+1)=a(n)+d)
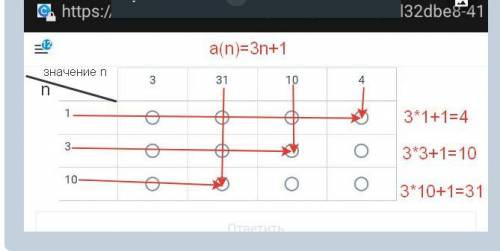
2) Арифметическая прогрессия может быть задана аналитическим При этом последовательность задается в виде формулы, и,подставляя в нее вместо переменной n, натуральные числа, возможно найти значение любого ее члена.
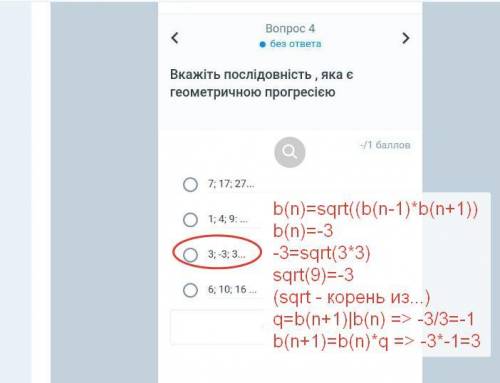
3) Чтобы определить является ли заданная последовательность геометрической прогрессией, можно воспользоваться формулой: b(n)=√(b(n-1))*b(n+1)) - значение члена геометрической прогрессии = корню из произведения предыдущего и последующего членов.
Решение во вложении
Определения к заданию
1 )Арифметическая прогрессия - это числовая последовательность, в которой каждый член, начиная со второго, равен сумме первого члена и разности d: a(n+1)=a(n)+d)
2) Арифметическая прогрессия может быть задана аналитическим При этом последовательность задается в виде формулы, и,подставляя в нее вместо переменной n, натуральные числа, возможно найти значение любого ее члена.
3) Чтобы определить является ли заданная последовательность геометрической прогрессией, можно воспользоваться формулой: b(n)=√(b(n-1))*b(n+1)) - значение члена геометрической прогрессии = корню из произведения предыдущего и последующего членов.
Решение во вложении



Уравнение касательной к графику функции y = f(x) в точке с абсциссой x = a имеет вид
y = f ' (a)*(x-a) + f (a).
а) f(x) = sin 2x, a = П/4
Итак, получим уравнение: у=1.
б) f(x) = 2 tg x/3, a = 0
Итак, получим уравнение: у=0+6(x-0), т.е.у=6х.