В решении.
Объяснение:
дитячий майданчик має форму прямокутника обнесений парканом обща довжина якого становить 54 м.Знайди довжини сторін цього майданчика якщо його площа становить 140 м2.
Детская площадка имеет форму прямоугольника, обнесена забором, общая длина которого составляет 54 м. Найти длины сторон этой площадки, если её площадь составляет 140 м².
a - длина прямоугольника.
b - ширина прямоугольника.
Р прямоугольника = 2(a + b) = 54 м.
S прямоугольника = a * b = 140 м².
Система уравнений:
2(a + b) = 54
a * b = 140
Разделить первое уравнение на 2 для упрощения:
a + b = 27;
Выразить а через b:
a = 27 - b;
Подставить выражение а во второе уравнение и вычислить b:
(27 - b) * b = 140
27b - b² - 140 = 0/-1
b² - 27b + 140 = 0, квадратное уравнение, ищем корни:
D=b²-4ac =729 - 560 = 169 √D=13
b₁=(-b-√D)/2a
b₁=(27-13)/2
b₁=14/2
b₁=7;
b₂=(-b+√D)/2a
b₂=(27+13)/2
b₂=40/2
b₂=20;
a = 27 - b;
a₁ = 27 - 7
a₁ = 20;
a₂ = 27 - 20
a₂ = 7;
Получили две пары решений: (20; 7) и (7; 20).
Так как длина прямоугольника обозначена а, за решение принять первую пару:
20 (м) - длина площадки.
7 (м) - ширина площадки.
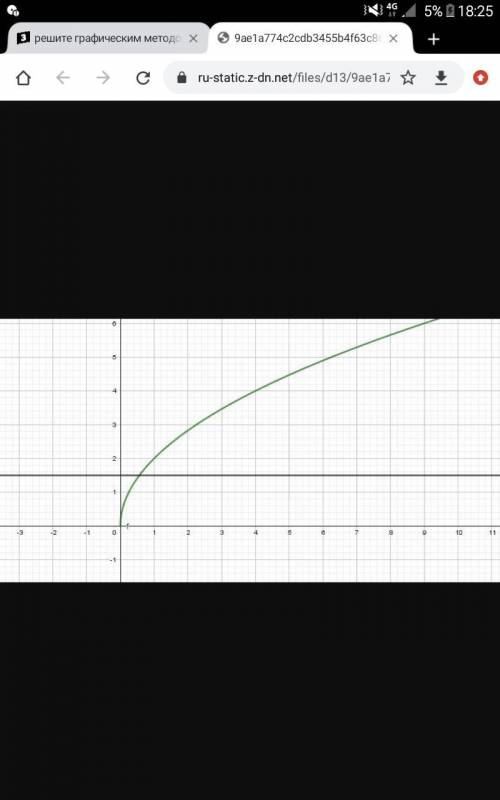
1) Построим графики функций и прямую параллельную оси ОХ
Графики пересекаются в точке (0.5625; 1.5), где x = 0.5625 - корень данного уравнения
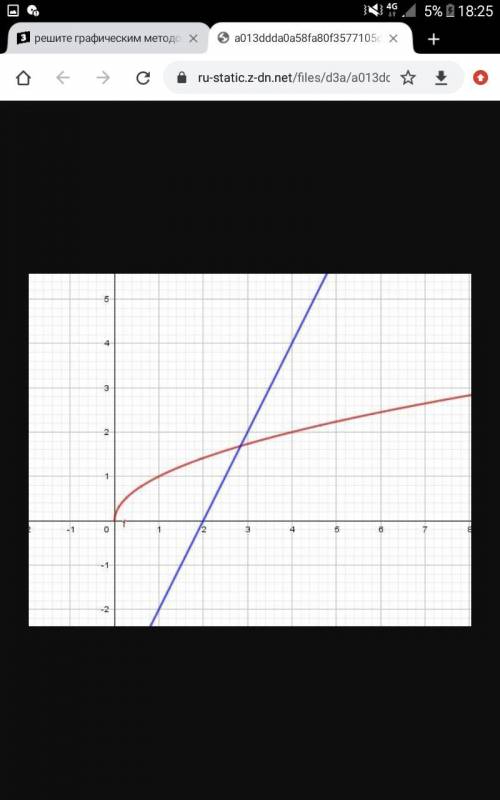
2) Построим график функции и прямую проходящую через точки (0;-4), (2;0). Отсюда абсцисса точки пересечения двух графиков
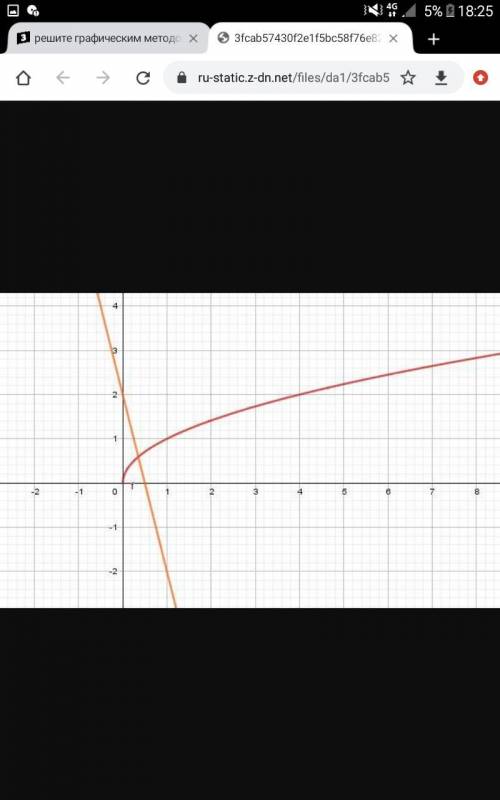
3) Построим график функции y = √x и прямую y = 2 - 4x, проходящую через точки (0;2), (1;-2). Абсцисса точки пересечения двух графиков равна
4) Построим график функции y = 0.4√x и прямую y = 1 - 2x, проходящую через точки (0;1), (1;-1). Абсцисса точки пересечения двух графиков равна
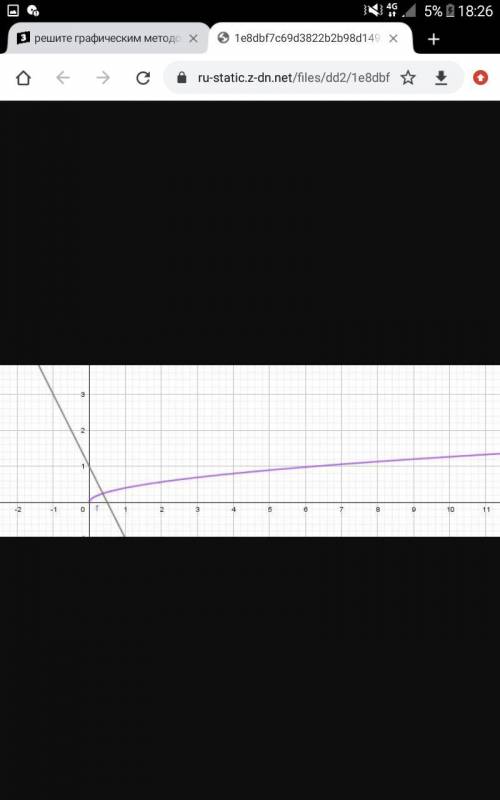
1-3, 2-4, 3-2, 4-1
Объяснение:
так надо