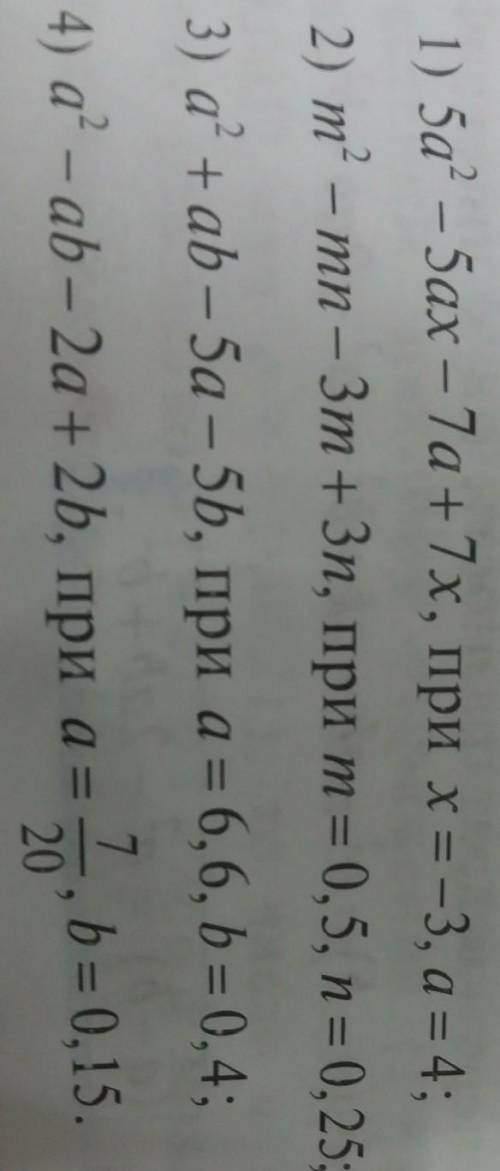
Любое выражение в квадрате принимает наименьшее значение 0. Сумма квадратов тоже принимает наименьшее значение 0.
Следовательно, наименьшее значение выражения 0. Чтобы выражение было равно 0, нужно, чтобы либо первое слагаемое было х, а второе -х; либо первое слагаемое -х, а второе х; либо оба слагаемых должны быть равны 0. Так как здесь сумма квадратов, то ни одно из слагаемых отрицательным быть не может => Оба слагаемых равны 0.
5х+4у+6=0 3х+4у+2=0
Выражаем 4у из обоих уравнений:
4у=-6-5х 4у=-2-3х
Приравниваем -6-5х=-2-3х
-2х=4
х=-2
Подставляем х в одно из уравнений:
4у=-2-3*(-2)
4у=4
у=1
а={3;-1;1} и b={0;2;1}, пусть перпендикулярный вектор с={x,y,z}
Тогда скалярное произведение ac=0, bc=0, то есть
3x- y+z =0
2y+z =0
x^2+y^2+z^2=1 (так как с - единичный вектор).
Решая систему из этих трех уравнений, получим, что
z=-2y (из второго)
x=y (из первого)
Подставим все в последнее, получим, что 6у^2=1, то есть у=+-1/(корень из 6),
тогда х=+-1/(корень из 6), z=-+2/(корень из 6).
ответ: (1/(корень из 6),1/(корень из 6 ),-2/(корень из 6))
и (-1/(корень из 6),-1/(корень из 6 ),2/(корень из 6))
1)91
2)0,125
3)11.2
4)-0.53
Объяснение:
1)5a^2-5ax-7a+7x, при x=-3, a=4
5*4^2-5*4*(-3)-7*4+7*(-3)=80-(-60)-28+(-21)=91
2)m^2-mn-3m+3n, при m=0,5, n=0,25
0,5*2-0,5*0,25-3*0,5+3*0,25=1-0,125-1,5+0,75=0,125
3)a^2+ab-5a-5b, при а=6,6, b=0,4
6,6^2+6.6*0.4-5*6.6-5*0.4=43.56+2.64-33-2=11.2
4)a^2-ab-2a+2b, при а=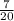 , b=0,15
, b=0,15