(см. объяснение)
Объяснение:
Первый :
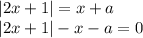
Рассмотрим функцию 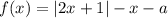 .
.
Тогда уравнение примет вид 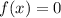 .
.
Заметим, что решающую роль на поведение функции (ее возрастание или убывание) всегда оказывает знак при 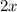 . Тогда функция убывает на промежутке
. Тогда функция убывает на промежутке ![\left(-\infty;\;-\dfrac{1}{2}\right]](/tpl/images/2004/3282/207f5.png) , а возрастает на
, а возрастает на 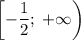 . Значит единственное решение достигается тогда и только тогда, когда
. Значит единственное решение достигается тогда и только тогда, когда 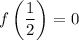 .
.
Получили уравнение:
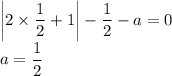
Итого при 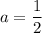 исходное уравнение имеет единственное решение.
исходное уравнение имеет единственное решение.
Второй :
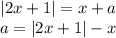
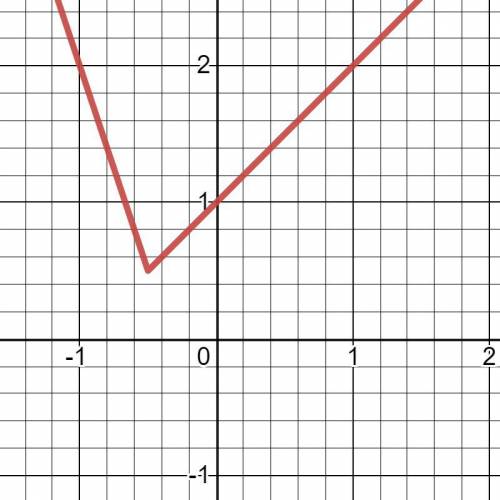
Построим график этого уравнения в координатах 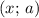 :
:
(см. прикрепленный файл)
Тогда ответом будет 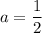 .
.
Третий :
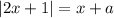
Знаем, что при 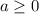 :
:
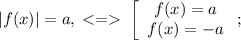
Тогда единственное решение возможно, только если 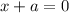 .
.
Получили уравнение:
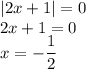
Так как 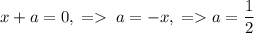 .
.
Задание выполнено!
Логарифмическая функция с основанием 5>1 возрастающая. Поэтому большему значению функции соответствует большее значение аргумента. С учетом ОДЗ неравенства получаем систему:
3x-2>25
3x>27
x>9
ответ. (9; +∞)
2)
Логарифмическая функция с основанием 0<1/2<1 убывающая. Большему значению функции соответствует меньшее значение аргумента. С учетом ОДЗ неравенства получаем систему:
4х+2>8
4x>8-2
4x>6
x>1,5
ответ. (1,5; +∞)
3)
Логарифмическая функция с основанием 0<1/2<1 убывающая. Большему значению функции соответствует меньшее значение аргумента. С учетом ОДЗ неравенства получаем систему:
ответ. [-1,5; 0,5)
4)Находим ОДЗ:
Логарифмическая функция с основанием 3>1- возрастающая. Поэтому большему значению функции соответствует большее значение аргумента. С учетом ОДЗ неравенства получаем систему:
Система не имеет решений
\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\
-----------------------------(-10)------------(3)------------
////////////////////////
множества не пересекаются