y = ax² + bx + c
y = x² + 2x + 1 = (x + 1)²
положительная парабола - значения, при которых функция принимает положительные значения
ну отрицательная соответственно отрицательные
1. наименьшее значение при a > 0 в вершине x0 = -b/2a = -2/2 = -1
наибольших нет, уходит в бесконечность
2. убывание - меньшему значению аргумента соответствует большеее значение функции
y(-3) = (-3+1)² = 4
y(-2) = (-2 + 1)² = 1
возрастание - большему значению аргумента соответствует меньшеее значение функции
y(2) = (2 + 1)² = 9
y(1) = (1 + 1)² = 4
3, y = (x + 1)² > 0 при x ∈(-∞, -1) U (-1, +∞)
y = 0 при x = -1
y < 0 нет
![D(y)=(0;\ 2].](/tpl/images/1860/7095/b9ff4.png)
Объяснение:
Для данной функции 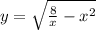 есть два ограничения на область определения: первое, возникающее из-за квадратного корня и требующее, чтобы подкоренное выражение было неотрицательным, а также второе, возникающее из-за дроби, требующее, чтобы знаменатель дроби не был нулевым.
есть два ограничения на область определения: первое, возникающее из-за квадратного корня и требующее, чтобы подкоренное выражение было неотрицательным, а также второе, возникающее из-за дроби, требующее, чтобы знаменатель дроби не был нулевым.
Получаем, что нужно решить неравенства:
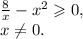
Решим первое:
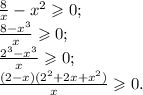
Разложив числитель на множители, мы можем решить неравенство методом интервалов. Выделим особые точки:
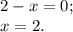
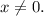
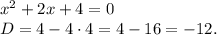
Корней нет. Точками для метода интервалов будут 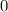 ,
, 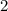 .
.
Для всех точек левее 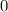 значение выражения будет отрицательным.
значение выражения будет отрицательным.
Для точек между 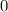 и
и 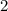 значение выражения будет положительным.
значение выражения будет положительным.
Для точек правее 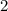 значение выражения будет отрицательным.
значение выражения будет отрицательным.
Получаем, что решением неравенства будет промежуток чисел от 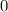 до
до 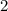 . Поскольку неравенство нестрогое, промежуток должен включать свои границы, однако по причине наличия в системе неравенства
. Поскольку неравенство нестрогое, промежуток должен включать свои границы, однако по причине наличия в системе неравенства 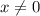 , исключающего из решения левую границу промежутка, итоговый промежуток будет иметь вид:
, исключающего из решения левую границу промежутка, итоговый промежуток будет иметь вид: ![(0;\ 2].](/tpl/images/1860/7095/ec6e5.png)
Это решение и является областью определения функции, то есть ![x \in (0;\ 2].](/tpl/images/1860/7095/bee93.png)
a ∈ (16/17; 2)
Объяснение:
(2 – a)x² – 3ax + 2a = 0
При a = 2 квадратное уравнение вырождается в линейное, а следовательно имеет единственный корень, что не соответствует условию задачи, поэтому 2 – a ≠ 0 и a ≠ 2.
У квадратного уравнения имеется два различных корня тогда и только тогда, когда дискриминант строго больше нуля.
D = (–3a)² – 4·(2 – a)·2a = 9a² – 16a + 8a² = 17a² – 16a = a·(17a – 16)
Корнями уравнения a·(17a – 16) = 0 являются числа a₁ = 0 и a₂ = 16/17, и поэтому D = a·(17a – 16) > 0 при a < 0 или a > 16/17.
Разделим обе части исходного уравнения на (2 – a), чтобы получить приведенное квадратное уравнение:
Полученное уравнение задает параболу, причем ветви параболы направлены вверх. Одновременно оба корня уравнения будут лежать с одной стороны от точки x = 0.5, когда f(0.5) > 0 (см. рисунок):
"Корнями" являются a₁ = –2 и a₂ = 2, неравенство выполняется при –2 < a < 2.
По теореме Виета значение 3a / (2 – a) равно сумме корней уравнения. Тогда M = 3a / (4 – 2a) является арифметическим средним корней и лежит ровно посередине между ними. Оба корня будут лежать справа от x = 0.5, когда их среднее M > 0.5 (см. рисунок):
"Корнями" являются a₁ = 0.5 и a₂ = 2, неравенство выполняется при 0.5 < a < 2.
Таким образом, корни уравнения (2 – a)x² – 3ax + 2a = 0 являются действительными и оба больше 0.5 при одновременном выполнении системы из трех условий:
1. дискриминант строго больше нуля ⇒ a ∈ (–∞; 0) ∪ (16/17; +∞),
2. для приведенного уравнения справедливо f(0.5) > 0 ⇒ a ∈ (–2; 2),
3. среднее значение корней приведенного квадратного уравнения больше 0.5 ⇒ a ∈ (0.5; 2).
Пересекая полученные интервалы, получаем ответ: a ∈ (16/17; 2).