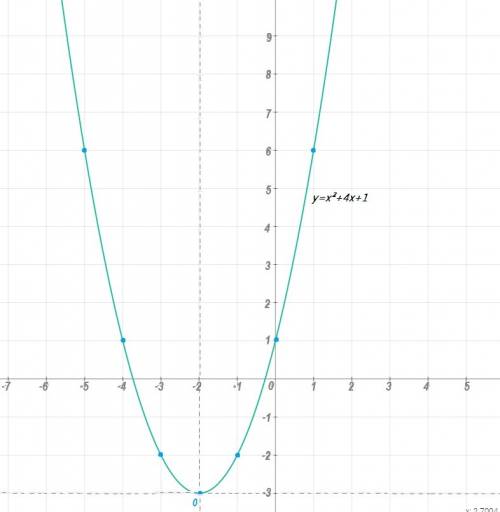
ДАНО: y = x² + 4*x + 1
ПОСТРОИТЬ ГРАФИК
РЕШЕНИЕ.
Преобразуем функцию к квадрату суммы.
y = x² + 4*x + 1 = (x² + 2*(2*x) + 4) - 4+1 = (x+2)² - 3 - прибавили и вычли 4.
Получили уравнение параболы у = х² со смещенной вершиной в точку А(-2;-3)
Для построения параболы используем точки (0;0), (1;1), (2;4), (3,9) и свойство параболы, что она чётная (парная). Заданную функцию начинаем строить из точки (-2;-3)
Рисунок с графиками в приложении.
1.
а)2х/3у;
б)(х+1)/х.
2.
а)(х-2)/х;
б)(ах²)/(8у²).
3. 8.
Объяснение:
1. Сократить дроби:
а)[16x(x-y)]/[24y(x-y)]=
сокращение (x-y) и (x-y) на (x-y), 16 и 24 на 8:
=2х/3у;
б)(х²+х)/х²=[x(x+1)]/x²=
сокращение х и x² на х:
=(х+1)/х.
2. Выполнить действия:
а)(14х-9)/17х+(3х-25)/17х=
=(14х-9+3х-25)/17х=
=(17х-34)/17х=
=[17(x-2)]/17x=
сокращение 17 и 17 на 17:
=(х-2)/х;
б)(ах+ау)/ху³ * х³у/(8х+8у)=
=[a(x+y)]/ху³ * х³у/[8(x+y)]=
Чтобы умножить дробь на дробь, нужно числитель первой дроби умножить на числитель второй дроби, а знаменатель первой дроби умножить на знаменатель второй дроби:
=[a(x+y)*х³у] / [ху³ *8(x+y)]=
сокращение (x+y) и (x+y) на (x+y), х и х³ на х, у и у³ на у:
=(ах²)/(8у²).
3. Найти значение выражения:
(у²-4у+4)/(у²-4) : (10у-20)/(у²+2у)= при у=80
В числителе первой дроби развёрнут квадрат разности, свернуть, в знаменателе разность квадратов, развернуть.
В числителе второй дроби вынести 10 за скобки, в знаменателе вынести у за скобки:
=(у-2)²/(у-2)(у+2) : [10(y-2)]/[y(y+2)]=
Чтобы разделить дробь на дробь, нужно числитель первой дроби умножить на знаменатель второй, а знаменатель первой умножить на числитель второй.
=[(у-2)(у-2)*y(y+2)] : [(у-2)(у+2)*10(y-2)]=
сокращение (у-2) и (у-2) на (у-2) 2 раза, (у+2) и (у+2) на (у+2)
=у/10=80/10=8.
a) функция - композиция дробно-рациональной
t(x)=1/(x-1) и показательной y=7^(t(x))
t(x)=1/(x-1) - непрерывна при х∈(-∞;1) U(1;+∞)
y=7^(t(x)) - непрерывна при t∈(-∞;+∞)
Значит и данная функция непрерывна при x∈(-∞;1) U(1;+∞)
Проверяем непрерывность в точке x=1
Находим предел слева: lim (x→1-0)7^(1/(x-1))=0
x→1-0 тогда (1/(x-1))→-∞
7^(-∞)→0
Находим предел справа:lim (x→1+0)7^(1/(x-1))=+∞
x→1+0 тогда (1/(x-1))→+∞
7^(+∞)→+∞
x=1- точка разрыва второго рода ( один из односторонних пределов - бесконечный)
б) y=x² непрерывна на (-∞;+∞), а потому непрерывна и на [0;1]
y=2x+3 непрерывна на (-∞;+∞), а потому непрерывна и на (1;2]
Значит, надо исследовать непрерывность в точке х=1
Находим предел слева: lim (x→1-0)x²=(1-0)²=1
Находим предел справа:lim (x→1+0)7=2·1+3=5
Предел слева не равен пределу справа.
Значит предел функции в точке не существует и потому
x=1- точка разрыва первого рода ( пределы конечны, но не равны, есть конечный скачок)
ТЕОРИЯ (это важно):
Сначала нужно найти начало координат, то есть вершину параболы с учётом её сдвига. Для этого находим координаты x₀, y₀ вершины O параболы (по осям OX и OY соответственно), вычисляем их по специальным формулам:Значит, O(-2;-3).
2. Построим график функции y=x². Строим таблицу значений:x=1 x=2 x=3
y=1 y=4 y=9
График на картинке
АЛГОРИТМ ПОСТРОЕНИЯ КВАДРАТИЧНОЙ ФУНКЦИИ y=ax²+bx+c:
Найти координаты начала координат (вершины параболы).Определить, из какой функции получена данная в условии функция.Строим таблицу значений для той функции, из которой получена данная нам в условии функция.Отмечаем на чертеже точку вершины параболы, построить оси.Построить и подписать параболу.