х=±3
Объяснение:
При сдвиге графика g(x)=x² на 9 единиц вниз получается график у=f(x)=x²-9.
Нули функции, когда у=0,
то есть 0=х²-9
х²-9=0
х²-3²=0
(х-3)(х+3)=0
х-3=0 или х+3=0
х=0+3 или х=0-3
х1=3 , х2=-3
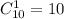а две другие - 
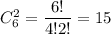По правилу произведения, всего треугольников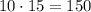 
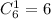а две другие - 
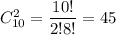По правилу произведения, всего таких треугольников - 6*45=270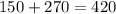
если сдвинуть график g(x)=x² вдоль оси ординат на 9 единиц вниз то получится график f(x)= х²-9
нули функции это точки в которых ордината равна нулю => у=0
тоесть
х²-9=0
х²=9
х1=-3; х2=3
это и есть ответ