1)
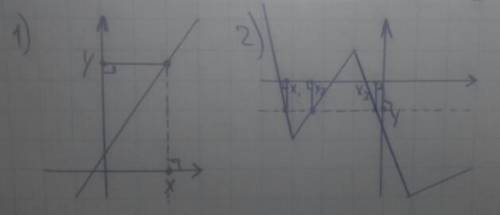
Дана абсцисса точки.
Найти ординату точки графика функции, с данной абсциссой.
На оси абсцисс из данной абсциссы проводим перпендикуляр к оси абс. Из точки, пересечения перпендикуляра с графиком функции, проводим перпедикуляр к оси ординат. Точка имеет ту же ординату, что и точка пересечения перпендикуляра с осью орд.
2)
Дана ордината точки.
Найти абсциссу точки(ек) графика функции, с данной ординатой.
На оси ординат из данной орд. проводим перпендикуляр к оси орд. Из точек, пересечения перпендикуляра с графиком функции, проводим перпедикуляры к оси абс. Точки имеют абсциссу, соответствующую точки пересечения перпендикуляра с осью абс.
периметр прямоугольника P=2(a+b)
площадь прямоугольника S=a*b.
Составим систему уравнений
2(a+b)=22 a+b=11 a=11-b
a*b=24 a*b=24 (11-b)*b=24
11b-b²=24
-b²+11b-24=0
D=11²-4*(-1)*(-24)=121-96=25
b=(-11-5)/(-2)=8 b=(-11+5)/(-2)=3
Решением задачи можно принять любой корень уравнения, допустим примем b=8 см, тогда сторона а=11-8=3 см.
Если за решение принять b=3 см, то а=8 см, то есть значения сторон прямоугольника не изменятся.
ответ: стороны прямоугольника 8 см и 3 см.