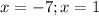
Объяснение:
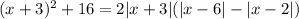
Выделим в левой части полный квадрат. Для этого прибавим к обеим частям уравнения выражение 
и перенесем слагаемое 
в левую часть:
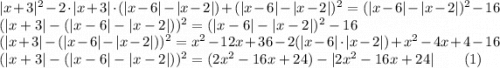
1) 
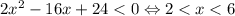
Тогда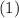 
примет вид
Левая часть неотрицательна. Правая часть, учитывая рассматриваемый интервал, строго отрицательна. Значит, корней на данном интервале нет.
2) 
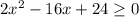
Возможны 2 случая:
2.1)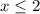 
Тогда 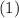примет вид
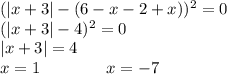
Оба корня принадлежат рассматриваемому интервалу, а значит являются корнями исходного уравнения.
2.2) 
Тогда 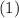примет вид
То есть корень не принадлежит рассматриваемому интервалу.
y=2x^2+4y=2x
2
+4 .
Уравнение параболы ищем в виде y=ax^2+bx+cy=ax
2
+bx+c .
Точка А(0,4) принадлежит параболе, значит её координаты удовлетворяют уравнению параболы . Подставим их в уравнение.
4=a\cdot 0^2+b\cdot 0+c\; \; \Rightarrow \; \; c=44=a⋅0
2
+b⋅0+c⇒c=4
Абсцисса вершины параболы по условию равна 0 и вычисляется по формуле:
x_{v}=-\frac{b}{2a}\; \; \Rightarrow \; \; \frac{-b}{2a}=0\; ,\; \; b=0x
v
=−
2a
b
⇒
2a
−b
=0,b=0
Уравнение принимает вид: y=ax^2+4y=ax
2
+4 .
Теперь подставим координаты точки В(-1,6) в уравнение параболы.
6=a\cdot (-1)^2+4\; \; \Rightarrow \; \; 6=a+4\; \; ,\; \; a=26=a⋅(−1)
2
+4⇒6=a+4,a=2
Итак, искомое уравнение имеет вид: y=2x^2+
а) 9a2 + 24a +16
б) 4b2 - 6ab + 9/4a2
в) 4a2 - b2
г) 1/9b4 - 4x2
Объяснение:
Там где после одночлена стоит число - это показатель степени
Пример:
9a2 2 -степень