Один тракторист может засеять за один день поле площадью 22,9 га. второй - на 8 га больше. сколько дней потребуется двум трактористам, чтобы засеять при совместной работе поле площадью 215,2 га? площадь поля
прямоугольной формы равна 28 га. его длина 700 м. вычислите ширину поля. постройте угол, градусная мера которого состав ляет 25% развернутого угла. из двух городов одновременно навстречу друг другу выехали два
велосипедиста. их скорости равны 11,5 км/ч и 13,5 км/ч. через 0,8 часа расстояние меж ду велосипедистами было 95,8 км. найдите расстоя ние между .

👇

Увидеть ответ

Ответ:

Kara2006kara

02.09.2021

1.Второй -22.9+8=30.9

разом вони - 30.9+22.9=53.8

днів потрібно - 215.2/53.8=4.

2. 1га = 10 000 м2

28га=280000м2

Ширина= 280000м2/700м=400м

3.Розділити розгорнутий кут на 4 рівні частини.

4. Швидкість зближення - 11.5+13.5=24км/ч

за 0.8 год вини проїхали 24*0.8=19.2км

відстань між містами - 95.8+19.2=115км

4,7(27 оценок)

Открыть все ответы

Ответ:

TamaraKengurs

02.09.2021

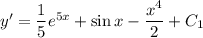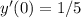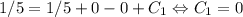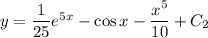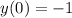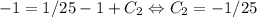1) Интегрируем обе части: $y' = \dfrac{1}{5}e^{5x}+\sin x-\dfrac{x^4}{2}+C_{1}$ . Поскольку y'(0) = 1/5 , то $1/5 = 1/5+0-0+C_{1} \Leftrightarrow C_{1} = 0$ . Интегрируем еще раз: $y = \dfrac{1}{25}e^{5x}-\cos x - \dfrac{x^{5}}{10}+C_{2}$ . Но поскольку y(0) = -1 , то $-1 = 1/25-1+C_{2} \Leftrightarrow C_{2} = -1/25$ . Следовательно, ответ: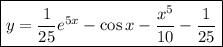 $\boxed{y = \dfrac{1}{25}e^{5x}-\cos x-\dfrac{x^{5}}{10}-\dfrac{1}{25}}$

2) Сделаем замену 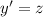y' = z . Тогда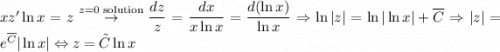 $xz'\ln x = z\stackrel{z=0\text{ solution}}{\to} \dfrac{dz}{z}=\dfrac{dx}{x\ln x} = \dfrac{d(\ln x)}{\ln x} \Rightarrow \ln|z| = \ln|\ln x|+\overline{C}\Rightarrow |z| = e^{\overline{C}}|\ln x| \Leftrightarrow z = \tilde{C}\ln x$

После обратной замены: 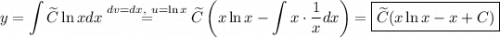$y = \displaystyle \int \widetilde{C}\ln x dx \stackrel{dv=dx,\ u=\ln x}{=} \widetilde{C}\left(x\ln x-\int x\cdot \dfrac{1}{x}dx\right) =\boxed{ \widetilde{C}(x\ln x - x+C)}$

3) Здесь снова делаем замену 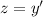z=y' . Тогда 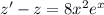$z' -z = 8x^2e^{x}$ . Решаем однородное уравнение: 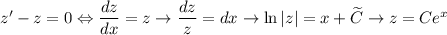$z' - z = 0 \Leftrightarrow \dfrac{dz}{dx} = z \to\dfrac{dz}{z} = dx \to \ln |z| = x+\widetilde{C} \to z = Ce^{x}$ . Применяем метод вариации постоянной, то есть ищем решение в виде 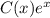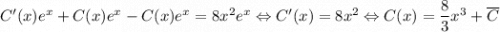$C(x)e^{x}$ : $C'(x)e^{x}+C(x)e^{x} - C(x)e^{x} = 8x^2e^{x} \Leftrightarrow C'(x) = 8x^2 \Leftrightarrow C(x) = \dfrac{8}{3}x^{3}+\overline{C}$ . Значит, 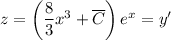$z = \left(\dfrac{8}{3}x^{3}+\overline{C}\right)e^{x} = y'$ . Здесь просто интегрируем. 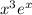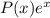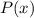Чтобы не делать несколько раз интегрирование по частям, можно понять, что первообразная $x^{3}e^{x}$ имеет вид $P(x)e^{x}$ , где P(x) -- некоторый полином. Тогда 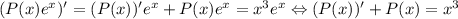$(P(x)e^{x})' = (P(x))'e^{x}+P(x)e^{x} = x^{3}e^{x} \Leftrightarrow (P(x))' +P(x) = x^{3}$ , то есть по сути, требуется решить еще один диффур, но можно поступить проще: 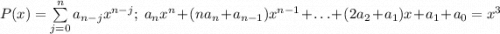$P(x) = \sum\limits_{j=0}^{n}a_{n-j}x^{n-j};\; a_{n}x^{n}+(na_{n}+a_{n-1})x^{n-1}+\ldots + (2a_{2}+a_{1})x+a_{1}+a_{0}=x^{3}$ , откуда 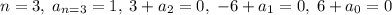$n=3,\;a_{n=3}=1,\; 3+a_{2} = 0,\; -6+a_{1}=0,\;6+a_{0}=0$ , следовательно, 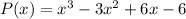$P(x) = x^{3}-3x^2+6x-6$ . Имеем: 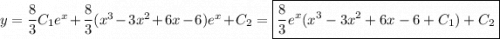$y = \dfrac{8}{3}C_{1}e^{x}+\dfrac{8}{3}(x^{3}-3x^2+6x-6)e^{x}+C_{2} = \boxed{\dfrac{8}{3}e^{x}(x^3-3x^2+6x-6+C_{1})+C_{2}}$ , где $C_{1} = \dfrac{3}{8}\overline{C}$ .

4,6(43 оценок)

Ответ:

alenajad

02.09.2021

Примем

а1- первое число

а2 - второе число

а3 - третье число

а4 - четвертое число

а5 - пятое число

тогда

а2=а1+1

а3=а2+1=а1+2

а4=а3+1=а1+3

а5=а4+4=а1+4

(а1)^2+(a2)^2+(a3)^2=(a4)^2+(a5)^2

(а1)^2+(а1+1)^2+(а1+2)^2=(а1+3)^2+(а1+4)^2

(а1)^2+(а1)^2+2*a1+1+(а1)^2+4*a1+4=(а1)^2+6*a1+9+(а1)^2+8*a1+16

(а1)^2+(а1)^2+2*a1+1+(а1)^2+4*a1+4-(а1)^2-6*a1-9-(а1)^2-8*a1-16=0

(а1)^2-8*a1-20=0

Квадратное уравнение, решаем относительно a1:
Ищем дискриминант:
D=(-8)^2-4*1*(-20)=64-4*(-20)=64-(-4*20)=64-(-80)=64+80=144;
Дискриминант больше 0, уравнение имеет 2 корня:
a1_1=10;
a1_2=-2.

Тогда

а2_1=а1_1+1=10+1=11

а3_1=а2_1+1=11+1=12

а4_1=а3_1+1=12+1=13

а5_1=а4_1+1=13+1=14

а2_2=а1_2+1=-2+1=-1

а3_2=а2_2+1=-1+1=0

а4_2=а3_2+1=0+1=1

а5_2=а4_2+1=1+1=2

Проверим:

10^2+11^2+12^2=13^2+14^2--->365=365

(-2)^2+(-1)^2+0^2=1^2+2^2--->5=5