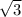sin(x).Похідна даної функції має вигляд: -sin(x)-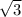cos(x)Знайдем критичні точки функції , коли похідна рівна 0. -sin(x) - 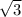*cos(x) = 0; → sin(x) + √3*cos(x)=0;(sin(x)/cos(x)) + √3*(cos(x)/cos(x))=0/cos(x);tg(x)+√3=0; → tg(x)= -√3; → x=arctg(-√3);x= -(π/3) + πn, де n ∈ Z.Знаходим значення функції в критичних точкахx= -(π/3); → y=cos(-π/3) - √3*sin(π/3)=(1/2) -√3*(-√3/2)=1/2 + 3/2=2;x=(2π/3); → y=cos(2π/3) -√3*sin(2π/3)==-(1/2) - √3*(√3/2)= -1/2 - 3/2=-2.Відповідь: найбільше значення функції у=2;найменше значення функції у=-2.
Объяснение:
1) (x - y)² + (x + y)²=х²-2ху+у²+х²+ху+у²=2х²+2у²
2) (x + y)² -(x - y)²=2у*2х=4ху
3) (2a + b)² - (2a - b)²=2b*4a=8ab
4) (2a+b)² + (2a - b)²=4а²+4аb+b²+4a²-4ab+b²=8a²+2b²