1. Длина площадки равна 15 м, ширина равна 7 м.
2. 3 упаковки.
Объяснение:
Площадь площадки равна 105 м².
1 сторона на 8 метров больше другой.
Бордюр в упаковках по 15 метров.
1. Вычислить значения сторон площадки,
2. Вычислить необходимое число упаковок для бордюра.
Решение.
1. Пусть одна сторона х м. Тогда вторая равна х+8 м.
S площадки равно х(х+8)=105 м².
х²+8х-105=0;
По теореме Виета
х1+х2=-8; х1*х2=-105;
х1= 7; х2= -15 --- не соответствует условию.
Одна сторона площадки равна 7 метров.
Вторая сторона равна 7+8=15 метров.
2. Периметр площадки равен
Р=2(а+b)=2(7+15)=44 метра
в одной упаковке 15 метров материала для бордюр.
Значит надо купить 44/15=2 14/15 упаковок
или, округленно, 3 упаковки
В обеих точках функция непрерывна
Объяснение:
Для ответа на данный вопрос найдём пределы слева и справа от указанных точек, если пределы совпадают, то функция в данной точке непрерывна, если не совпадают, то функция имеет разрыв первого рода, а если хотя бы один из пределов равен бесконечности или не существует, то в данной точке функция имеет разрыв второго рода.
для x = 0
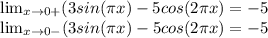
Как видим, пределы слева и справа совпадают, следовательно f(0) непрерывна
для x = 1
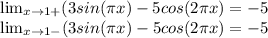
Снова видим, что пределы совпадают, следовательно и при f(1) функция непрерывна.
1 36
2. 8!/ (5!*(8-5)!)=40320/ 720=56
3!/(2!*(3-2)!)=3
p=3/56
3 А1-попал первый стрелок р(А1)=0.7
А2-попал второй стрелок р(А2)=0.8
В1-первый стрелок не попал р(В1)=1-р(А1)=0.3
В2-второй стрелок не попал р(В2)=1-р(А2)=0.2
С-попал только один из стрелков
р(С)=р(А1)*р(В2)+р(А2)*р(В1)=0.38