№1 Постройте график функции y=2(x-5)2+1, запишите все свойства. №2. Запишите формулу задающую функцию, которая получится при перемещении графика функции у= 2х2 на 2 единицы влево и на 3 единицы вниз.
График - парабола с вершиной в точке (5;1) , ветви вверх, ось симметрии х=5 . Получена из параболы путём растяжения вдоль оси ОУ в 2 раза, затем она смещена вдоль оси ОХ вправо на 5 единиц и вдоль оси ОУ вверх на 1 единицу .
Пересечение с осью ОХ нет ⇒ при .
Пресечение с осью ОУ в точке .
Убывает при , возрастает при .
Точка минимума минимальное значение функции .
График - парабола, с вершиной в точке (2;-3) , ветви вверх, ось симметрии х= -2 . Получена при перемещении графика вдоль оси ОХ влево на 2 единицы и вдоль оси ОУ вниз на 3 единицы .
Третий закон Кеплера гласит - квадраты периодов обращения планет вокруг Солнца относятся, как кубы больших полуосей орбит планет. Проверим закон Кеплера на планете Земля. Принято, что расстояние от планета Земля до планеты Солнце равно 1 астрономическая единица (а. е.) и также считают, что Солнце - центр нашей планетарной системы, следовательно оно относительно нас недвижимо и формула (Тз/Тс)²=(Аз/Ас)³ превращается в формулу (Тз/1)²=(Аз/1)³ ⇒ (Тз)²=(Аз)³ ⇒ Тз=√(Аз)³. Так как на планете Земля Аз (период вращения вокруг планеты Солнце) 1 а. е. ⇒ Тз=√1³=1, то есть ≈365 земных дней. Теперь можно вычислить "звёздный период вращения планеты Марс" вокруг планеты Солнце: Тм=√(1,5)³≈1,837 земного года≈1,837*365≈671 земной день.
Пусть скорость течения равна x км/ч, тогда скорость против течения (18-x) км/ч, а скорость по течению - (18+x) км/ч . Время, затраченное против течения равно 8/(18-x) ч, а по течению - 8/(18+x) ч.
График - парабола с вершиной в точке (5;1) , ветви вверх, ось симметрии х=5 . Получена из параболы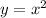 путём растяжения вдоль оси ОУ в 2 раза, затем она смещена вдоль оси ОХ вправо на 5 единиц и вдоль оси ОУ вверх на 1 единицу .
путём растяжения вдоль оси ОУ в 2 раза, затем она смещена вдоль оси ОХ вправо на 5 единиц и вдоль оси ОУ вверх на 1 единицу .
Пересечение с осью ОХ нет ⇒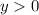 при
при 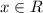 .
.
Пресечение с осью ОУ в точке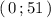 .
.
Убывает при![x\in (-\infty ;\, 5\ ]](/tpl/images/1657/0857/c774b.png) , возрастает при
, возрастает при 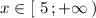 .
.
Точка минимума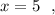 минимальное значение функции
минимальное значение функции 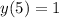 .
.
График - парабола, с вершиной в точке (2;-3) , ветви вверх, ось симметрии х= -2 . Получена при перемещении графика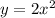 вдоль оси ОХ влево на 2 единицы и вдоль оси ОУ вниз на 3 единицы .
вдоль оси ОХ влево на 2 единицы и вдоль оси ОУ вниз на 3 единицы .