Дробь 
является неправильной рациональной дробью, так как степени многочленов в числителе и в знаменателе одинаковые и равны 1. Значит можно выделить целую и дробную часть неправильной дроби. Так как в знаменателе стоит многочлен 1 степени (линейная ф-ция) х+1, то и в числителе выделим х+1. Для этого надо вынести за скобки коэффициент (-5), который стоит перед х, и записать в скобках (х+1). Так как -5(х+1)=-5х-5, то , чтобы выражение не изменилось, надо добавить (+5), получим:
.
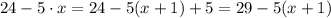Если в дальнейшем надо записать целую и дробную части неправильной рац. дроби, то
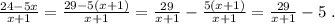
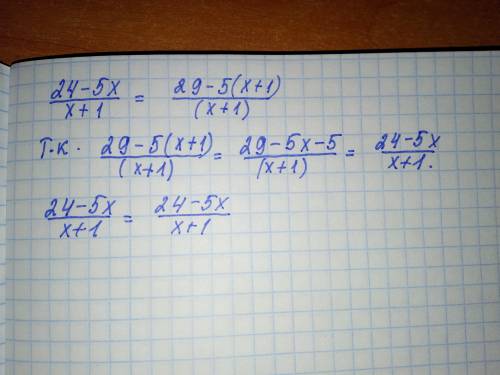
1)2a + bc + 2b + 3bd
2)3mx - my + 3nx - ny
3)ab - ac - 5b + 5c
4)ax + bx - ay - by + az +bz
5)a + b + c(a + b)
6)m - n + p(m - n)
7)x + 3a(x + y) + y
8)x + 2a(x - y) - y
9)2m(m - n) + m - n
10)4q(p - 1) + (p - 1)
11)2m(m - n) + n - m
12)4q(p - 1) + 1 - p
13)ab + bc - 2ad - 2bd
14)ac - 3bd + ad - 3bc
15)2bx - 3ay - 6by + ax
16)5ay + 3bx + ax - 15by
17)18a2 - 27ab + 14ac - 21bc
18)10x2 + 10xy + 5x + 5y
19)35ax + 24xy - 20ay - 42x2
20)48xz2 + 32xy2 - 15yz2 - 10y3