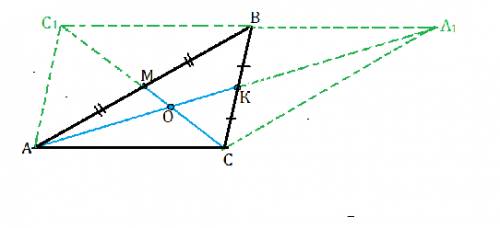
Пусть дан т-к АВС.
Продлим медианы на их длину ( см. рис)
По свойству диагоналей параллелограмма
АА1²+ВС²=2(АВ²+АС²)
и
СС1²+АВ²=2(АС²+ВС²)
Пусть АВ=с, ВС=а
Составим систему уравнений:
[(2*6√7)²+a²=2(c²+14²)
[(2*3√7)²+c²=2(14²+a²)
⇒
[ а²-2с²=2*14² -144*7
[-2а²+с²=2*14²-36*7 домножим на 2 обе стороны этого уравнения.
Сложим уравнения системы:
[а²-2с=2*14² -144*7
[-4а²+2с²=4*14²-72*7
-3а²=6*14²-216*7⇒
а²=112
а=4√7
Подставим найденное значение а в уравнение
а²-2с²=2*14² -144*7 ⇒
112+144*7-2*196=2 с²
с²=364
с=2√91
АВ=2√91
ВС=4√7
---------
Задачу можно решить по т. косинусов.
Медианы треугольника точкой пересечения делятся в отношении 2:1, считая от вершины.
Тогда АО=4√7, CO=2√7
Из ∆ АОС
АС²=АО²+СО²-2*АО*СО*cos ∠АОС
cos ∠АОС=(АС²-АО²+СО²):(-2*АО*СО)
cos ∠АОС=[14²-(4√7)²-(2√7)²]:[-2*(4√7)*(2√7]
cos ∠АОС= -56:2*56= -1/2 - это косинус 120º
В ∆ СОК ∠ СОК =180°-120°=60°
ОК=АК:3=2√7
ОК=ОС, угол СОК=60°⇒
∆ СОК - правильный, СК=2√7,
ВС=2 СК=4√7
В Δ АМО ∠ МОА=∠ СОК=60°
АМ²=МО+АО-2*МО*АО*cos∠АОМ
АМ²=(√7)²+(4√7)²-2*(√7)*(4√7)*1/2*cos∠АОМ
АМ²=7+16*7-2*4*7*1/2
АМ²=91
АМ=√91
AB=2√91
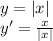
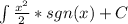 , хотя по сути можно упрощение сделать. Это лишь формальности
, хотя по сути можно упрощение сделать. Это лишь формальности ![(x)=x-[x]](/tpl/images/0249/7769/6c968.png) , где
, где ![[x]](/tpl/images/0249/7769/6e538.png) целая часть числа.
целая часть числа. 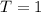 , это видно из графика .
, это видно из графика . 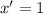
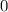 до
до 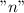 , то площадь этих треугольников , равна
, то площадь этих треугольников , равна 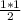 , если же перейти к примеру то
, если же перейти к примеру то ![\int\limits^n_0 \frac{[x]}{2}^2+\frac{(x)}{2}^2 +C](/tpl/images/0249/7769/ec562.png)
1)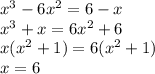
2)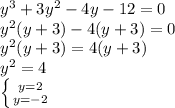
3)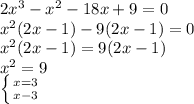
4)
5)
6)