a³+8-a²-2a
Розкладіть на множники

В решении.
Объяснение:
Найдите целые решения неравенства:
-х²+10х-21>0
Приравнять к нулю и решить квадратное уравнение:
-х² + 10х - 21 = 0/-1
х² - 10х + 21 = 0
D=b²-4ac =100 - 84 = 16 √D=4
х₁=(-b-√D)/2a
х₁=(10-4)/2
х₁=6/2
х₁=3;
х₂=(-b+√D)/2a
х₂=(10+4)/2
х₂=14/2
х₂=7.
Уравнение квадратичной функции, график - парабола, ветви направлены вниз, пересекают ось Ох в точках х= 3 и х= 7.
Решение неравенства: х∈(3; 7).
Неравенство строгое, значения х= 3 и х= 7 не входят в решение, поэтому целые решения неравенства: 4; 5; 6.
Пусть C — первая деталь окажется стандартной. Гипотезы:
H₁ - деталь изготовлена первым заводом;
H₂ - деталь изготовлена вторым заводом;
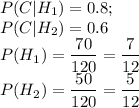
Вероятность события А по формуле полной вероятности
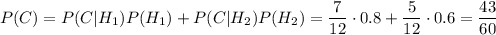
По формуле Байеса, вероятность того, что эта деталь изготовлена первым заводом, равна:
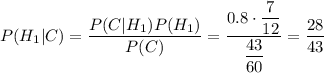
Аналогично, пусть В — вторая деталь окажется стандартной. Так как одна деталь уже вынута, то в партии остается 119 лампочек, из них 69 изготовлены на первом заводе.
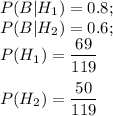
По формуле полной вероятности, вероятность события В:
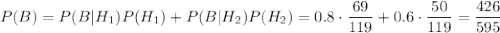
По формуле Байеса, вероятность того, что эта деталь изготовлена первым заводом, равна:
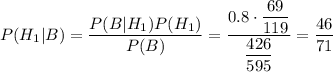
По теореме умножения, вероятность того, что наудачу взятые две лампочки являются стандартными, равна
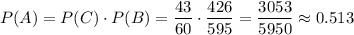
По теореме умножения, вероятность того, что обе лампочки изготовлены на первом заводе, при условии что событие А произошло, равна:
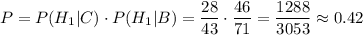
(a+2)*(a^2-2a+4)-a*(a+2)
(a+2)*(a^2-2a+4-a)
(a+2)*(a^2-3a+4)