График функции
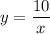
Для того чтобы отпределить принадлежит ли точка данному графику функции нужно подставить координату х в заданную функцию, вычилить значение у и сравнить
1) А(-0,05; -200)
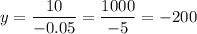
видим что у=-200 и координата у точки А совпадают. Значит точка А принадлежит данному графику
2) В(-0,1; 100)

Видим что у= -100 а координата у точки В равна 100
Значит точка В не лежит на графике данной функции
3) С(400; 0,25)

И опять видим что 0,025≠0,25
Значит точка С не принадлежит данному графику
4) D(500; -0.02)
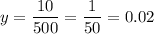
и опять видим что 0,02≠-0,02
Значит точка D не принадлежит данному графику
Чтобы найти в каких иксах пересекаются 2 графика функций приравняем функции друг к другу и решим получившееся уравнение.
x^2-4x+3 = x-1
x^2-5x+4 = 0
Дискриминант считаем по формуле, он равен 9, корень из него соответственно 3
Корни считаем по формуле:
x1 = (5-3)/2 = 1
x2 = (5+3)/2 = 4
Теперь ищем ординаты точек пересечений, для этого подставляем найденные иксы в любую из наших функций (проще во вторую):
y = 1-1 = 0
y = 4-1 = 3
Ну и среднее арифметическое этих ординат равно (0+3)/2 = 3/2