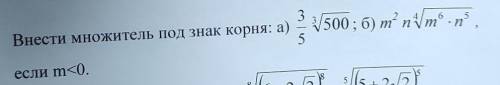
V3)
Используя тригонометрическое тождество cos(a - b) = cos(a)cos(b) + sin(a)sin(b) и условие соsα соsß, получаем:
cos(a - b) = cos(a)cos(ß) + sin(a)sin(ß) = cos(α)cos(ß) + sin(α)sin(ß) = cos(α - ß)
Тогда √√2 cos(a - b) = √√2 cos(α - ß).
V4)
Используя тригонометрические тождества cos(a + b) = cos(a)cos(b) - sin(a)sin(b) и sin(2θ) = 2sin(θ)cos(θ), получаем:
3 cos(a + ß) = 3(cos(a)cos(ß) - sin(a)sin(ß)) = 3cos(a)cos(ß) - 3sin(a)sin(ß) = 3(cos(a)cos(ß) - sin(a)sin(ß))sin(α)sin(ß) / (sin(α)sin(ß))
= 3(sin(α)cos(ß) + cos(α)sin(ß))sin(α)sin(ß) / (sin(α)sin(ß)) = 3(sin^2(α)cos(ß) + cos^2(α)sin(ß)) = 3(sin^2(α) + cos^2(α))sin(ß) = 3sin(ß)
Таким образом, 3 cos(a + ß) = 3sin(ß)
Обозначим производительность кондитерской "Буратино" как x кг шоколада в час. Тогда производительность кондитерской "Ассоль" будет равна (x + 6) кг шоколада в час.
Из условия задачи мы знаем, что кондитерская "Ассоль" выполняет заказ на 228 кг шоколада на 19 часов быстрее, чем кондитерская "Буратино". Это можно выразить уравнением:
228 / (x + 6) = 228 / x + 19
Решим это уравнение:
228x = 228(x + 6) + 19x(x + 6)
228x = 228x + 1368 + 19x^2 + 114x
0 = 19x^2 + 114x - 1368
0 = x^2 + 6x - 72
0 = (x + 12)(x - 6)
Из этого уравнения мы находим, что x = -12 или x = 6. Отрицательное значение не имеет смысла, поэтому производительность кондитерской "Буратино" составляет 6 кг шоколада в час. ответ: 6 кг шоколада в час.
Объяснение:
a)![\frac{3}{5} \sqrt[3]{500}=\sqrt[3]{(\frac{3}{5})^3*500}=\sqrt[3]{\frac{27}{125}*500 }=\sqrt[3]{108}](/tpl/images/1669/6350/ba26e.png)
б)![m^2*n\sqrt[4]{m^6*n^5}=\sqrt[4]{(m^2)^4*n^4*m^6*n^5} =\sqrt[4]{m^{14}*n^9}](/tpl/images/1669/6350/324fb.png)
Вот так вот.