Есть свойство о соотношении углов и сторон тр-ка: против большего угла лежит большая сторона и против меньшего угла лежит меньший угол, соответственно против большей стороны лежит больший и против меньшей стороны лежит меньший угол.
Т.е. нам дан △ABC, в котором дано следующее неравенство углов: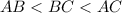 
. Соответственно, если сторона AC - наибольшая, то ∠B - наибольший, т.к. по свойству он лежит против большей стороны AC.
Такая же история получается и с меньшим углом △ABC. Т.е. поскольку сторона AB - наименьшая, то напротив лежащий ∠C - наименьший опять-таки по свойству. Ну и соответственно ∠A посередине.
ответ:
1. (-7b⁶ⁿ+15p³ⁿ))²=(-7b⁶ⁿ)²+2*(-7b⁶ⁿ)*(15p³ⁿ)+(15p³ⁿ)²=
49b¹²ⁿ-210b⁶ⁿ*p³ⁿ+225p⁶ⁿ
2. 36ⁿ-2*24ⁿ+16ⁿ=(6ⁿ)²-2*6ⁿ*4ⁿ+(4ⁿ)²=(6ⁿ-4ⁿ)²
3. Выделим полный квадрат x²+4x+19=х²+2*х*2+4+15=(х+2)²+15- сумма двух выражений, одно неотрицательно, это (х+2)², наименьшее свое значение оно приобретает, когда х+2=0, т .е., когда х=-2, все остальные его значения больше нуля, отрицательным быть не может. И второе выражение - постоянное - число.= 15, оно положительно. Т.е. получаем окончательно, что выражение x²+4x+19 приобретает наименьшее значение при х=-2, и оно равно 0+15=15
Объяснение:
(x-13)² + 125 = (x+12)²
x² - 26x + 169 + 125 = x² + 24x + 144
x² - x² - 26x - 24x = 144 - 125 - 169
-50x = -150
x = -150/(-50)
x = 3
Проверка:
(3-13)² + 125 = (3+12)²
(-10)² + 125 = 15²
100+125 = 225
225 = 225
ответ: при х=3.